[비선형 자료구조] 트리

트리(Tree)

• 노드와 링크로 구성된 자료구조
• 계층적 구조를 나타낼 때 사용
  • 폴더 구조(디렉토리,서브 디렉토리)
  • 조직도, 가계도 등..

트리의 구조

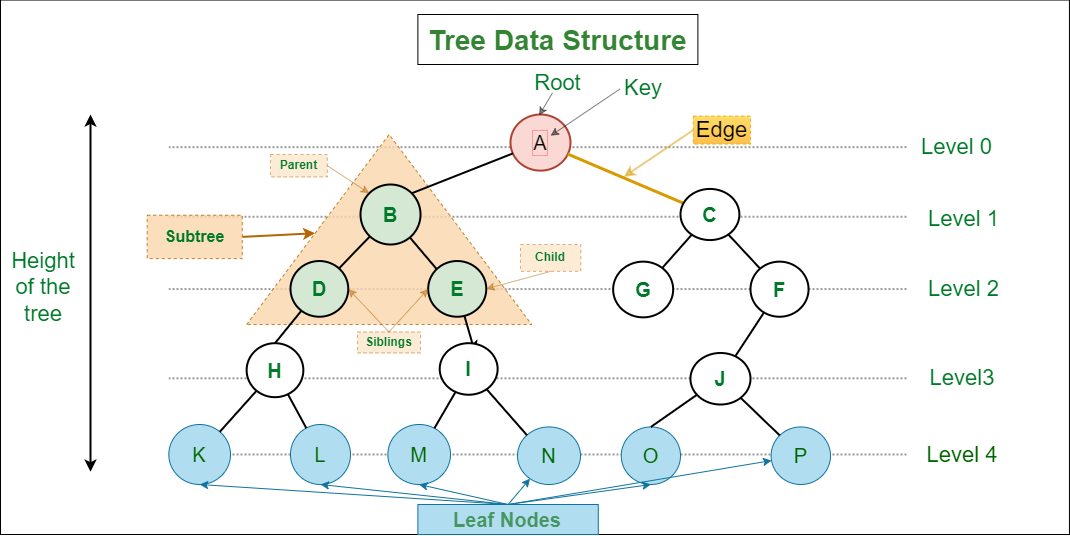
• 노드(Node): 트리 구조의 자료 값을 담고 있는 단위
• 에지(Edge): 노드 간의 연결선 (=link, branch)
• 루트 노드(Root): 부모가 없는 노드, 가장 위의 노드
• 잎새 노드(Leaf): 자식이 없는 노드 (=단말)
• 내부 노드(Internal): 잎새 노드를 제외한 모든 노드
• 부모(Parent): 연결된 두 노드 중 상위의 노드
• 자식(Child): 연결된 두 노드 중 하위의 노드
• 형제(Sibling): 같은 부모를 가지는 노드
• 깊이(Depth): 루트에서 어떤 노드까지의 간선의 수
• 레벨(Level): 트리의 특정 깊이를 가지는 노드 집합
• 높이(Height): 트리에서 가장 큰 레벨 값(이미지의 높이 : 4)
• 크기(Size): 자신을 포함한 자식 노드의 개수
• 차수(Degree): 각 노드가 지닌 가지의 수(A의 차수: 2 / F의 차수: 1)
• 트리의 차수: 트리의 최대 차수

---

트리의 특징

• 하나의 노드에서 다른 노드로 이동하는 경로는 유일하다.
• 노드가 N개인 트리의 Edge수는 n-1개
• Acyclic (Cycle - X)
• 모든 노드는 서로 연결되어 있어야한다.
• 하나의 Edge를 끊으면 2개의 Sub-Tree로 분리된다.

이진 트리(Binary Tree)

• 각 노드는 최대 2개의 자식을 가질 수 있다.
• 자식 노드는 좌우를 구분
  • 왼쪽 자식: 부모 노드의 왼쪽 아래
  • 오른쪽 자식: 부모 노드의 오른쪽 아래

이진 트리 종류

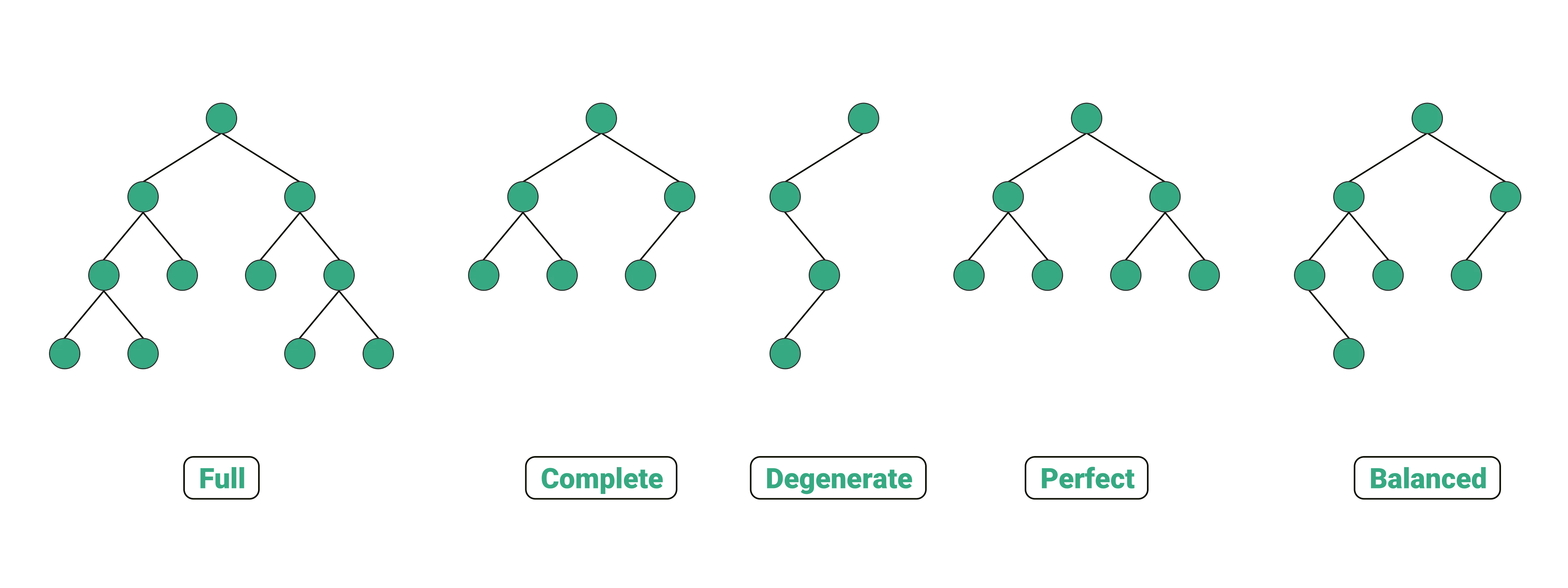
• 포화 이진 트리(Perfect Binary Tree)
  • 모든 레벨에서 노드들이 꽉 채워져 있는 트리
• 완전 이진 트리(Complete Binary Tree)
  • 마지막 레벨을 제외하고 노드들이 모두 채워져 있는 트리
• 정 이진 트리(Full Binary Tree)
  • 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
• 편향 트리(Skewed Binary Tree) = 사향 이진 트리(Degenerate Binary Tree)
  • 한쪽으로 기울어진 트리
• 균형 이진 트리(Balanced Binary Tree)
  • 모든 노드의 좌우 서브 트리 높이가 1이상 차이 나지 않는 트리

이진 트리 특징

• 포화 이진 트리의 높이가 h일 때 노드의 수는 2^h+1 - 1개
• 포화(or완전) 이진 트리의 노드가 N개 일 때 높이는 $log_2$N
• 이진 트리의 노드가 N개 일 때 최대 가능 높이는 N-1

이진 트리의 순회

• 모든 노드를 빠뜨리거나 중복하지 않고 방문하는 연산
• 순회 종류는 4가지
  • 전위 순회,중위 순회,후위 순회(DFS)
  • 레벨 순회(BFS)

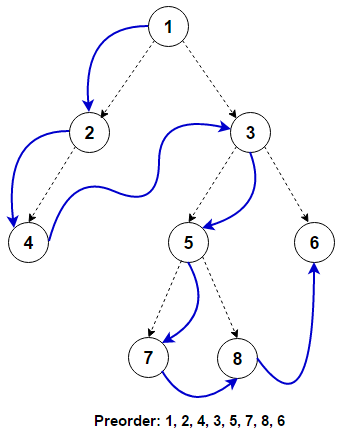
전위 순회

• Preorder Traversal

• 방문 순서: 현재 노드 -> 왼쪽 노드 -> 오른쪽 노드

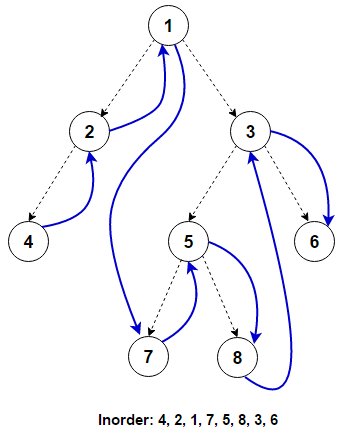
중위 순회

• Inorder Traversal

• 방문 순서: 왼쪽 노드 -> 현재 노드 -> 오른쪽 노드

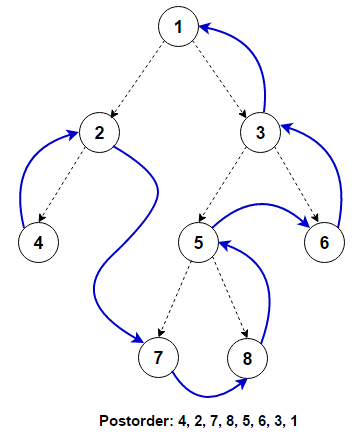
후위 순회

• Postorder Traversal

• 방문 순서: 왼쪽 노드 -> 오른쪽 노드 -> 현재 노드

레벨 순회

• Levelorder Traversal

• 방문 순서: 위쪽 레벨부터 왼쪽 노드 -> 오른쪽 노드

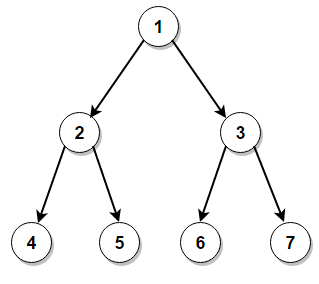
이진 트리 구성

• 배열 : 레벨 순회 순으로 배열을 구성

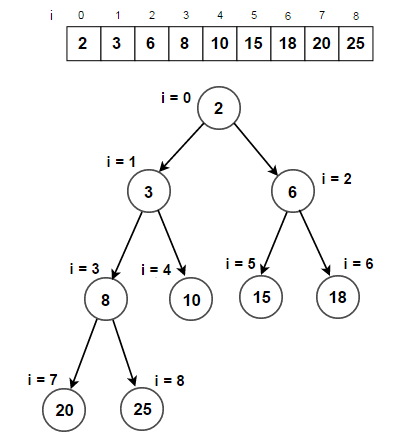
• 연결 리스트 : 값과 간선을 관리하기 위한 노드로 연결 리스트 구성

이진 트리 구현(Array)

class BinaryTree {
    char[] arr;

    public BinaryTree(char[] arr) {
        this.arr = arr;
    }

    public void preOrder(int idx) { //전위 순회(preOrder)
        System.out.print(this.arr[idx]+" ");
        int left = 2 * idx + 1;
        int right = 2 * idx + 2;

        if(left < this.arr.length){
            this.preOrder(left);
        }
        if(right < this.arr.length){
            this.preOrder(right);
        }
    }

    public void inOrder(int idx) { //중위 순회(inOrder)
        int left = 2 * idx + 1;
        int right = 2 * idx + 2;

        if(left < this.arr.length){
            this.inOrder(left);
        }

        System.out.print(this.arr[idx]+" ");

        if(right < this.arr.length){
            this.inOrder(right);
        }
    }
    public void postOrder(int idx) { //후위 순회(postOrder)
        int left = 2 * idx + 1;
        int right = 2 * idx + 2;

        if(left < this.arr.length){
            this.postOrder(left);
        }
        if(right < this.arr.length){
            this.postOrder(right);
        }

        System.out.print(this.arr[idx]+" ");
    }

    public void levelOrder(int idx){ //레벨 순회(levelOrder)
        for (int i = 0; i < this.arr.length; i++) {
            System.out.print(arr[i]+" ");
        }
        System.out.println();
    }
}

이진 트리 구현(Linked List)

import java.util.LinkedList;
import java.util.Queue;

class Node {
    char data;
    Node left;
    Node right;
    Node parent;

    public Node(char data, Node left, Node right) {
        this.data = data;
        this.left = left;
        this.right = right;
    }

    public Node(char data, Node left, Node right, Node parent) {
        this.data = data;
        this.left = left;
        this.right = right;
        this.parent = parent;
    }
}

class BinaryTree {
    Node head;

    public BinaryTree() {
    }

    public BinaryTree(Node head) {
        this.head = head;
    }

    public BinaryTree(char[] arr) {
        Node[] nodes = new Node[arr.length];
        for (int i = 0; i < arr.length; i++) {
            nodes[i] = new Node(arr[i], null, null, null);
        }

        for (int i = 0; i < arr.length; i++) {
            int left = 2 * i + 1;
            int right = 2 * i + 2;

            if (left < arr.length) {
                nodes[i].left = nodes[left];
                nodes[left].parent = nodes[i];
            }

            if (right < arr.length) {
                nodes[i].right = nodes[right];
                nodes[right].parent = nodes[i];
            }
        }

        this.head = nodes[0];
    }

    // 전위 순회(Pre-Order Traversal)
    public void preOrder(Node node) {
        if (node == null) {
            return;
        }
        System.out.print(node.data + " ");
        this.preOrder(node.left);
        this.preOrder(node.right);
    }

    //중위 순회(In-Order Traversal)
    public void inOrder(Node node) {
        if (node == null) {
            return;
        }

        this.inOrder(node.left);
        System.out.print(node.data + " ");
        this.inOrder(node.right);
    }

    //후위 순회(Post-Order Traversal)
    public void postOrder(Node node) {
        if (node == null) {
            return;
        }

        this.postOrder(node.left);
        this.postOrder(node.right);
        System.out.print(node.data + " ");
    }

    //레벨 순회(Level-Order Traversal)
    public void levelOrder(Node node) {
        Queue<Node> queue = new LinkedList<>();
        queue.add(node);

        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            System.out.print(cur.data + " ");

            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }

    //노드 검색
    public Node searchNode(char data) {
        Queue<Node> queue = new LinkedList<>();
        queue.add(this.head);

        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            if (cur.data == data) {
                return cur;
            }
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        return null;
    }

    public Integer checkSize(char data) {
        Node node = this.searchNode(data);

        Queue<Node> queue = new LinkedList<>();
        queue.add(node);
        int size = 1; // 자기자신포함
        while (!queue.isEmpty()) {
            Node cur = queue.poll();

            if (cur.left != null) {
                queue.offer(cur.left);
                size++;
            }
            if (cur.right != null) {
                queue.offer(cur.right);
                size++;
            }
        }
        return size;
    }
}

public class Tree {
    public static void main(String[] args) {
        //Test Code
        char[] arr = new char[10];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = (char) ('A' + i);
        }

        BinaryTree bt = new BinaryTree(arr);

        System.out.println("==Pre-Order==");
        bt.preOrder(bt.head);
        System.out.println();

        System.out.println("==In-Order==");
        bt.inOrder(bt.head);
        System.out.println();

        System.out.println("==Post-Order==");
        bt.postOrder(bt.head);
        System.out.println();

        System.out.println("==Level-Order==");
        bt.levelOrder(bt.head);
        System.out.println();

        // Root node
        System.out.println("Root: " + bt.head.data);

        // B's child node
        Node B = bt.searchNode('B');
        if (B.left != null) {
            System.out.println("B -> left child: " + B.left.data);
        }
        if (B.left != null) {
            System.out.println("B -> right child: " + B.right.data);
        }

        // F's parent node
        Node F = bt.searchNode('F');
        System.out.println("F -> parent: " + F.parent.data);

        // Leaf node
        System.out.print("Leaf node: ");
        for (int i = 0; i < arr.length; i++) {
            Node cur = bt.searchNode((char) ('A' + i));

            if (cur.left == null && cur.right == null) {
                System.out.print(cur.data + " ");
            }
        }
        System.out.println();

        // E's Depth
        Node E = bt.searchNode('E');
        Node cur = E;
        int cnt = 0;
        while (cur.parent != null) {
            cur = cur.parent;
            cnt++;
        }
        System.out.println("E depth: " + cnt);


        // Level2 Node
        System.out.print("Level2 Node: ");
        for (int i = 0; i < arr.length; i++) {
            Node target = bt.searchNode((char) ('A' + i));
            cur = target;
            cnt = 0;
            while (cur.parent != null) {
                cur = cur.parent;
                cnt++;
            }
            if (cnt == 2) {
                System.out.print(target.data + " ");
            }
        }
        System.out.println();

        // Height
        int maxCnt = Integer.MIN_VALUE;
        for (int i = 0; i < arr.length; i++) {
            Node target = bt.searchNode((char) ('A' + i));
            cur = target;
            cnt = 0;
            while (cur.parent != null) {
                cur = cur.parent;
                cnt++;
            }

            if (maxCnt < cnt) {
                maxCnt = cnt;
            }
        }
        System.out.println();

        // B's Size
        int size = bt.checkSize('B');
        System.out.println("B size = "+size);
    }
}

트리 연습 문제

• 문제1)

  종이를 반으로 접었을 때, 안으로 파인 부분은 0, 볼록 튀어나온 부분은 1이라고 하자.
  종이를 접을 때는 오른쪽에서 왼쪽으로 접는다.
  종이를 N번 접었을 때의 접힌 상태를 출력하는 문제를 작성하세요.
  

  입출력 예시
  입력: 1 / 출력: 0
  입력: 2 / 출력: 0, 0, 1
  입력: 3 / 출력: 0, 0, 1, 0, 0, 1, 1

public class Solution {
    public static void solution(int n) {
        //In-order 포화이진트리
        int[] binaryTree = new int[(int) Math.pow(2, n)];

        binaryTree[0] = 0;
        for (int i = 0; i < (int) Math.pow(2, n - 1) - 1; i++) {
            binaryTree[i * 2 + 1] = 0;
            binaryTree[i * 2 + 2] = 1;
        }

        inOrder(binaryTree, 0);
        System.out.println();
    }

    public static void inOrder(int[] arr, int idx) {
        int left = 2 * idx + 1;
        int right = 2 * idx + 2;
        if (left < arr.length - 1) {
            inOrder(arr, left);
        }
        System.out.print(arr[idx] + " ");
        if (right < arr.length - 1) {
            inOrder(arr, right);
        }
    }
}

• 문제2)

  각각의 에지에 가중치가 있는 포화 이진 트리가 있다.
  루트에서 각 리프까지의 경로 길이를 모두 같게 설정하고 모든 가중치들의 총합이 최소가 되도록 하는 프로그램을 작성하세요.

class BinaryTree {
    int h;
    int[] arr;
    int result;

    public BinaryTree(int h, int[] w) {
        this.h = h;
        arr = new int[(int) Math.pow(2, h + 1)];
        result = 0;
        /*
        초기값 2 설정이유 :
        1.초기값0은 사용안함
        2.포화이진트리에서 노드의 갯수는 7갠데 간선의 갯수는 (노드-1개)
        간선의 갯수가 필요한 것이기 때문에 초기값은 2부터 시작
         */
        for (int i = 2; i < (int) Math.pow(2, h + 1); i++) {
            arr[i] = w[i - 2];
        }
    }

    public int dfs(int idx, int h) {
        if (this.h == h) {
            result += arr[idx];
            return arr[idx];
        }

        int left = dfs(idx * 2, h + 1);
        int right = dfs(idx * 2 + 1, h + 1);
        result += arr[idx] + Math.abs(left - right);
        return arr[idx] + Math.max(left, right);
    }
}

public class Solution {
    public static void solution(int h, int[] w) {
        BinaryTree bt = new BinaryTree(h, w);
        bt.dfs(1,0);
        System.out.println(bt.result);
    }
}