[비선형 자료구조] 힙

힙(Heap)

• 완전 이진 트리 형태

  • 중복 값 허용

  • 반 정렬

    • 상태부모 노드와 자식 노드의 크기에 대한 우선순위는 보장하지만 형제 노드는 보장X

• 최소값 또는 최대값을 빠르게 찾아내는데 유용한 자료 구조

  • 최대 힙(Max Heap) : 부모 노드의 키가 자식 노드의 키보다 크거나 같은 형태

  • 최소 힙(Min Heap) : 부모 노드의 키가 자식노드의 키보다 작거나 같은 형태

힙 삽입

• 트리의 가장 끝 위치에 데이터 삽입
• 부모 노드와 키 비교한 후 작을 경우 부모자리와 교체(반복)

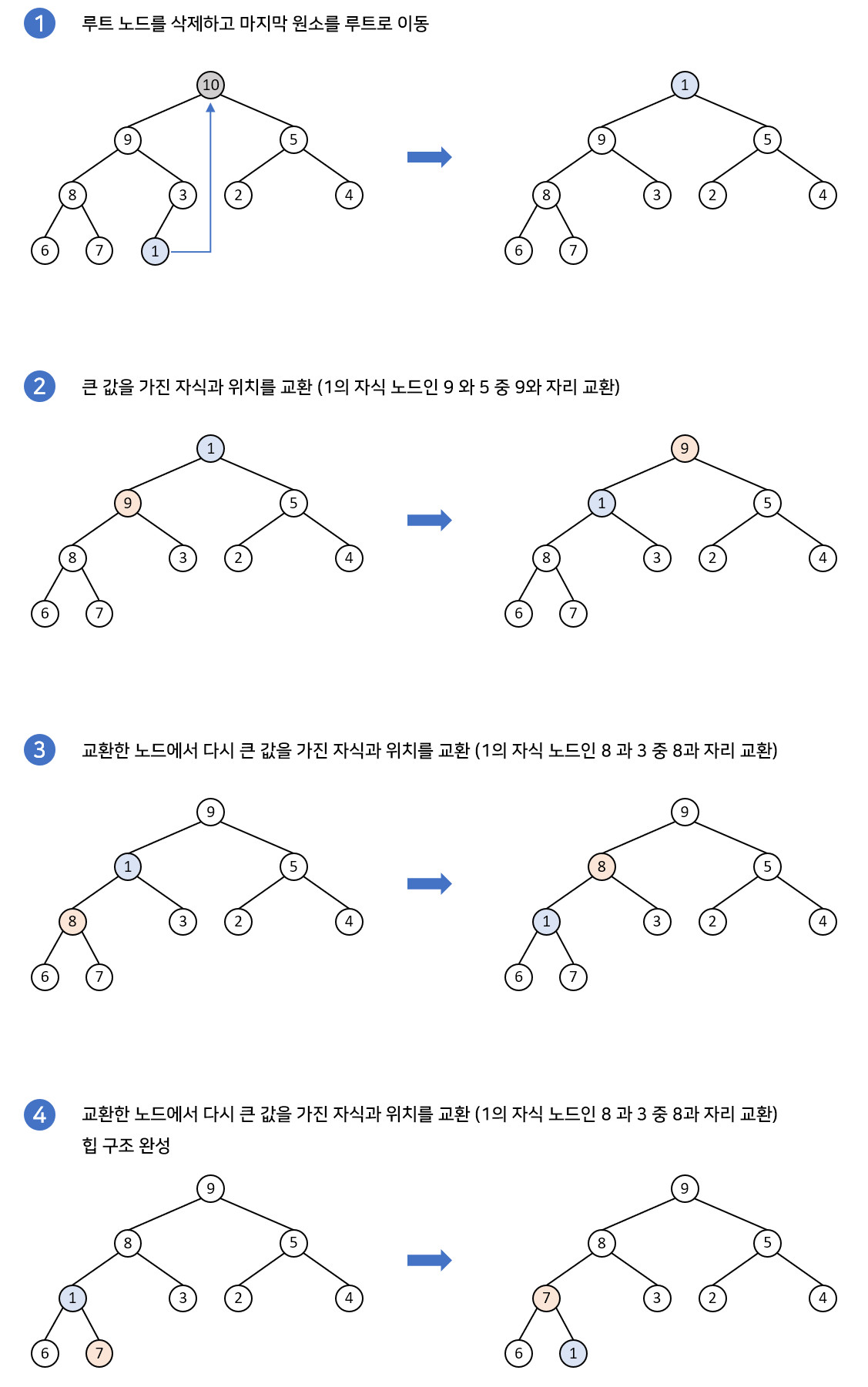
힙 삭제

• 최상위 노드 반환 및 삭제
• 가장 마지막 위치의 노드를 최상위 노드로 위치 시킴
• 자식 노드 중 작은 값과 비교 후 부모 노드가 더 크면 자리 교체(반복)

힙 구현

• Min Heap과 Max Heap 은 부등호 수정으로 간단하게 변경할 수 있다.

import java.util.ArrayList;

class Heap {
    ArrayList<Integer> heap;

    public Heap() {
        this.heap = new ArrayList<>();
        this.heap.add(0); //더미데이터를 추가하여 1번부터 시작할 수있게 설정
    }

    public void insert(int data) {
        heap.add(data);

        int cur = heap.size() - 1;
        //Min Heap일경우
        while (cur > 1 && heap.get(cur / 2) > heap.get(cur)) {
        //Max Heap일 경우
        //while (cur > 1 && heap.get(cur / 2) < heap.get(cur)) {
            int parentValue = heap.get(cur / 2);
            heap.set(cur / 2, data);
            heap.set(cur, parentValue);

            cur /= 2;
        }
    }

    public Integer delete() {
        if (heap.size() == 1) {
            System.out.println("Heap is empty");
            return null;
        }

        int target = heap.get(1);
        heap.set(1, heap.get(heap.size() - 1));
        heap.remove(heap.size() - 1);

        int cur = 1;
        while (true) {
            int leftIdx = cur * 2;
            int rightIdx = cur * 2 + 1;
            int targetIdx = -1;

            if (rightIdx < heap.size()) { //자식 노드가 둘다 있는 경우
                //Min Heap일 경우
                targetIdx = heap.get(leftIdx) < heap.get(rightIdx) ? leftIdx : rightIdx;
                //Max Heap일 경우
                //targetIdx = heap.get(leftIdx) > heap.get(rightIdx) ? leftIdx : rightIdx;
            } else if (leftIdx < heap.size()) { ///자식 노드가 하나 있는 경우
                targetIdx = leftIdx;
            } else { //부모노드만 있거나 리프노드일 경우
                break;
            }

            //Min Heap일 경우
            if (heap.get(cur) < heap.get(targetIdx)) {
            //Max Heap일 경우
            //if (heap.get(cur) > heap.get(targetIdx)) {
                break;
            } else {
                int parentValue = heap.get(cur);
                heap.set(cur, heap.get(targetIdx));
                heap.set(targetIdx, parentValue);
                cur = targetIdx;
            }
        }
        return target;
    }

    public void printTree() {
        for (int i = 1; i < this.heap.size(); i++) {
            System.out.print(this.heap.get(i) + " ");
        }
        System.out.println();
    }
}