[비선형 자료구조] 이진 탐색 트리
이진 탐색 트리(Binary Search Tree)
아래의 규칙으로 구성 된 이진 트리
- 왼쪽 자식 노드의 키는 부모 노드의 키보다 작음
- 오른쪽 자식 노드의 키는 부모 노드의 키보다 큼
- 각각의 서브 트리도 이진 탐색 트리를 유지
- 중복된 키를 허용하지 않음
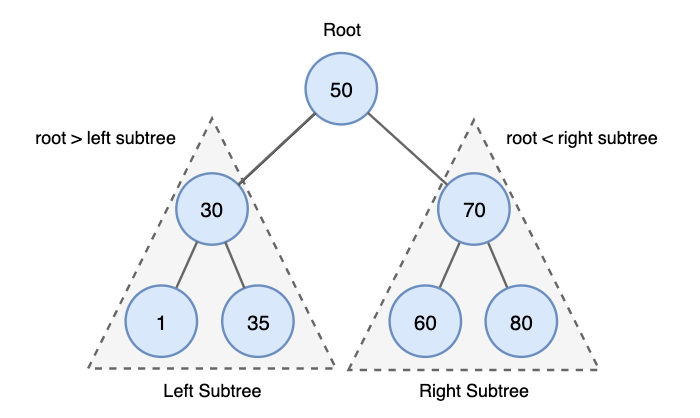
이진 탐색 트리의 특징
-
이진 탐색 트리 규칙에 의해 데이터가 정렬됨
-
이진 트리에 비해 탐색이 빠름(균형 유지 필요)
- 시간복잡도 : 균형상태 - O(logN) / 비균형상태 - O(N)
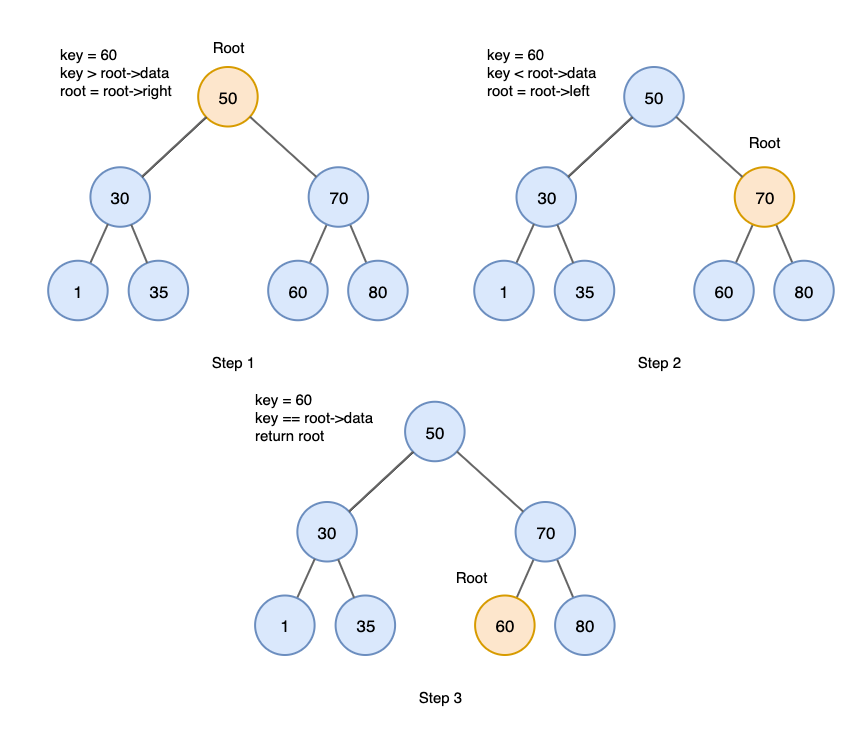
이진 탐색 트리 - 탐색
- 찾고자 하는 데이터를 루트 노드부터 비교 시작
- 대소 비교를 하여 찾는 데이터가 작으면 왼쪽, 크면 오른쪽 노드로 이동
- 찾는 데이터가 없으면 null 반환
- 어떤 데이터를 찾더라도 최대 트리 높이 만큼의 탐색이 이루어짐
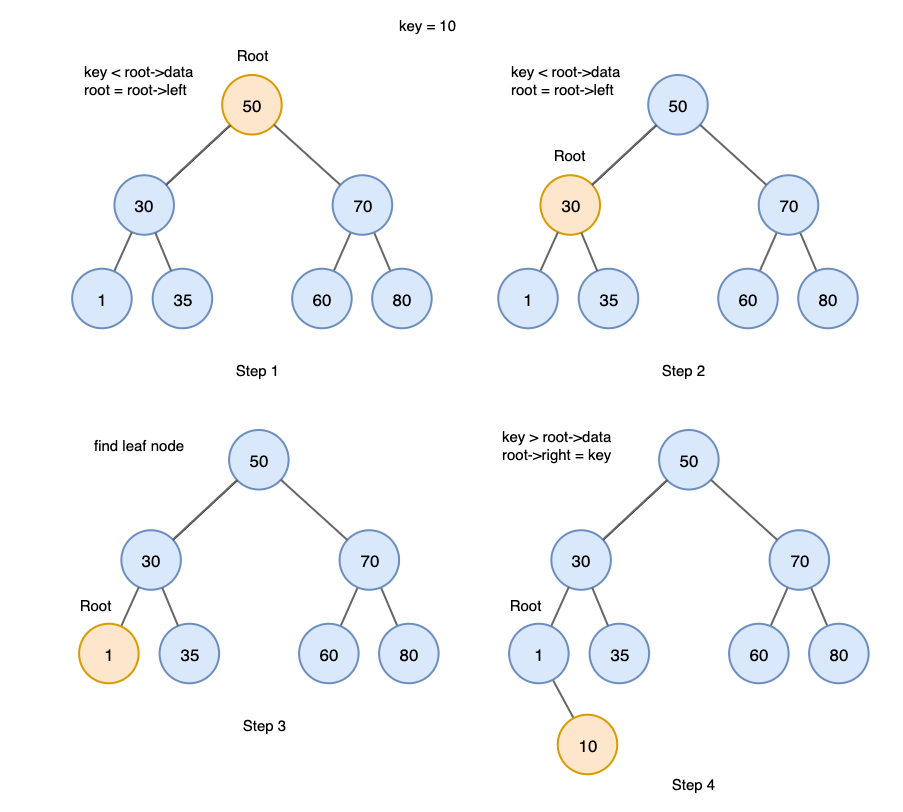
이진 탐색 트리 - 삽입
- Root부터 비교 시작 (중복 키 발견 시 노드 추가하지 않고 종료)
- 삽입할 키가 현재 노드의 키보다 작으면 왼쪽으로 크면 오른쪽으로 이동
- Leaf 노드에 도달 후 키 비교하여 작으면 왼쪽 크면 오른쪽에 삽입
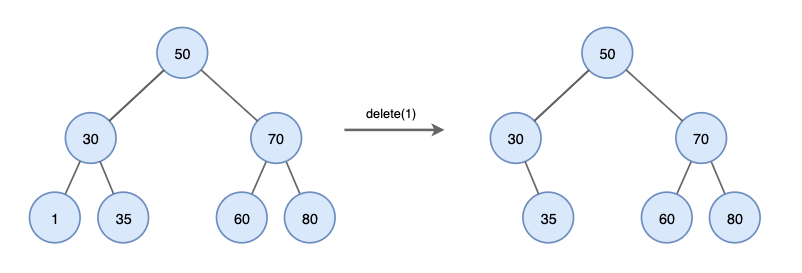
이진 탐색 트리 - 삭제
-
삭제 대상 노드가 leaf 노드인 경우
-
삭제 대상 노드 삭제
-
부모 노드의 해당 자식 링크 null로 변경
-
- 삭제 대상 노드에 자식 노드가 하나 있는 경우
- 자식 노드를 삭제 대상 노드의 부모 노드에 연결
- 삭제 대상 노드 삭제
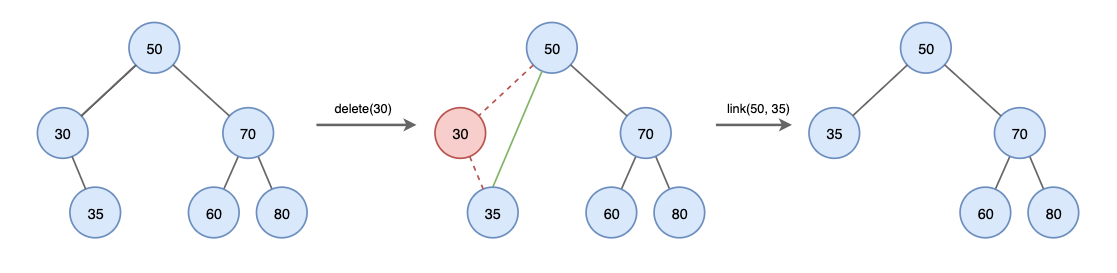
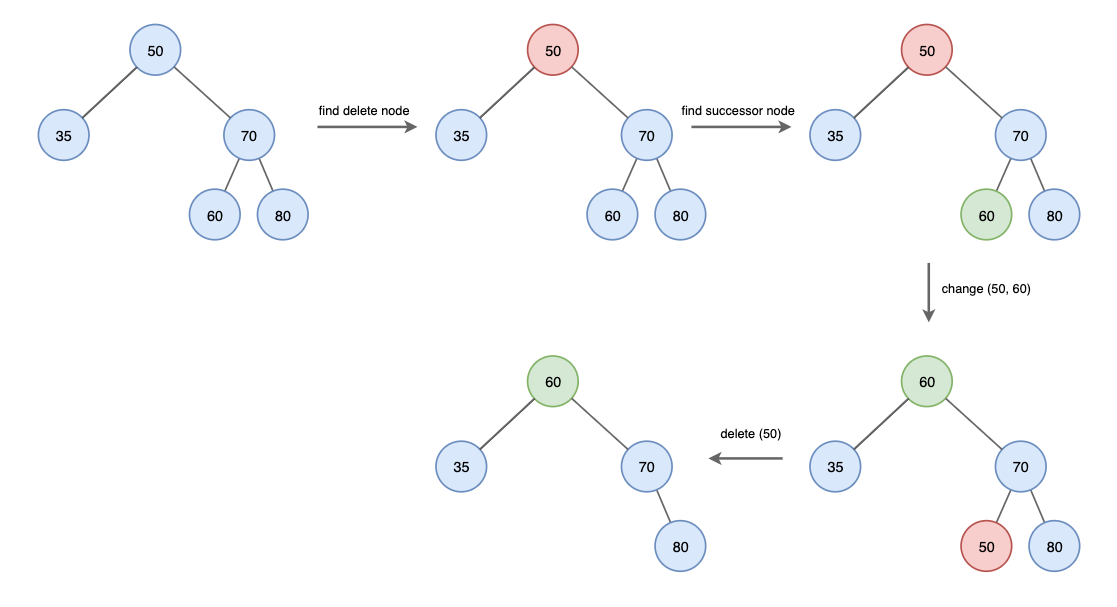
- 삭제 대상 노드에 자식 노드가 둘인 경우
- i) 삭제 대상 노드에서 왼쪽 서브 트리에서 가장 큰 노드 선택
- ii) 삭제 대상 노드의 오른쪽 서브 트리에서 가장 작은 노드 선택
- i 또는 ii에서 선택한 노드를 삭제 대상 노드 위치로 올림
- 위로 올리는 과정에서 다른 자식노드들의 링크 연결작업 진행 후 삭제 대상 노드 삭제
이진 탐색 트리 구현(List)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
class Node {
int key;
Node left;
Node right;
Node(int key, Node left, Node right) {
this.key = key;
this.left = left;
this.right = right;
}
}
class BinarySearchTree {
Node head;
BinarySearchTree(int key) {
this.head = new Node(key, null, null);
}
//데이터 추가
public void addNode(int key) {
if (this.head == null) {
this.head = new Node(key, null, null);
} else {
Node cur = this.head;
while (true) {
Node pre = cur;
if (key < cur.key) {
cur = cur.left;
if (cur == null) {
pre.left = new Node(key, null, null);
break;
}
} else {
cur = cur.right;
if (cur == null) {
pre.right = new Node(key, null, null);
break;
}
}
}
}
}
//데이터 삭제
public void removeNode(int key) {
Node parent = null; // 부모 노드
Node successor = null; // 지우고 변경해줘야하는 후계자를 가리킬 변수
Node predecessor = null; // successor 의 부모를 가리킬 노드
Node child = null; // successor의 자식노드 여부를 확인할 변수
Node cur = this.head;
while (cur != null) {
if (key == cur.key) {
break;
}
parent = cur;
if (key < cur.key) {
cur = cur.left;
} else {
cur = cur.right;
}
}
if (cur == null) {
System.out.println("key에 해당하는 노드가 없습니다.");
return;
}
// Leaf 노드인 경우
if (cur.left == null && cur.right == null) {
if (parent == null) { //트리에 노드 1개바께 없는 경우
this.head = null;
} else {
if (parent.left == cur) {
parent.left = null;
} else {
parent.right = null;
}
}
}
// 자식 노드가 하나인 경우
else if (cur.left != null && cur.right == null || cur.left == null && cur.right != null) {
if (cur.left != null) {
child = cur.left;
} else {
child = cur.right;
}
if (parent == null) { //루트노드인데 자식노드가 1개만 있는 경우
this.head = child;
} else {
if (parent.left == cur) {
parent.left = child;
} else {
parent.right = child;
}
}
} else { // 자식 노드가 둘인 경우(좌측에서 가장 큰 노드를 찾기)
predecessor = cur;
successor = cur.left;
while (successor.right != null) {
predecessor = successor;
successor = successor.right;
}
predecessor.right = successor.left;
successor.left = cur.left;
successor.right = cur.right;
if (parent == null) {
this.head = successor;
} else {
if (parent.left == cur) {
parent.left = successor;
} else {
parent.right = successor;
}
}
}
}
}
이진 탐색 트리 구현(재귀)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Node {
int key;
Node left;
Node right;
Node(int key, Node left, Node right) {
this.key = key;
this.left = left;
this.right = right;
}
}
class BinarySearchTree {
Node head;
BinarySearchTree(int key) {
this.head = new Node(key, null, null);
}
//데이터 추가
public Node addNodeRecursive(Node cur, int key) {
if (cur == null) {
return new Node(key, null, null);
}
if (key < cur.key) {
cur.left = addNodeRecursive(cur.left, key);
}else {
cur.right = addNodeRecursive(cur.right,key);
}
return cur;
}
//데이터 삭제
public Node removeNodeRecursive(Node cur, int key) {
if (cur == null) {
return null;
}
if (key < cur.key) {
cur.left = removeNodeRecursive(cur.left, key);
} else if (key > cur.key) {
cur.right = removeNodeRecursive(cur.right, key);
} else {
if (cur.left == null) {
return cur.right;
} else if (cur.right == null) {
return cur.left;
} else {
Node predecessor = cur;
Node successor = cur.left;
while (successor.right != null) {
predecessor = successor;
successor = successor.right;
}
predecessor.right = successor.left;
cur.key = successor.key;
}
}
return cur;
}
}
균형 이진 탐색 트리
- Balanced Binary Search Tree
- 노드의 삽입와 삭제가 일어날 때 균형을 유지하도록 하는 트리
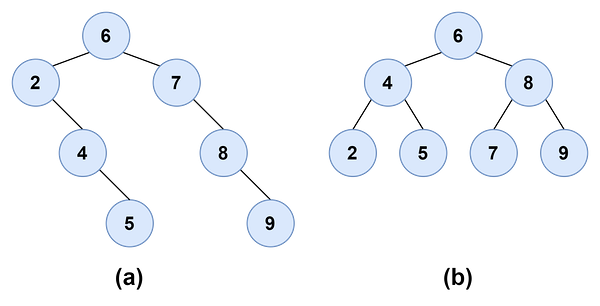
- 데이터의 삽입에 따라 편향트리(a)가 될 수도 있는데 이것을 이진 탐색 트리(b)로 조정
- AVL 트리, Red-Black 트리
AVL 트리
- 노드가 삽입, 삭제될 때 균형을 체크하고 유지하는 트리
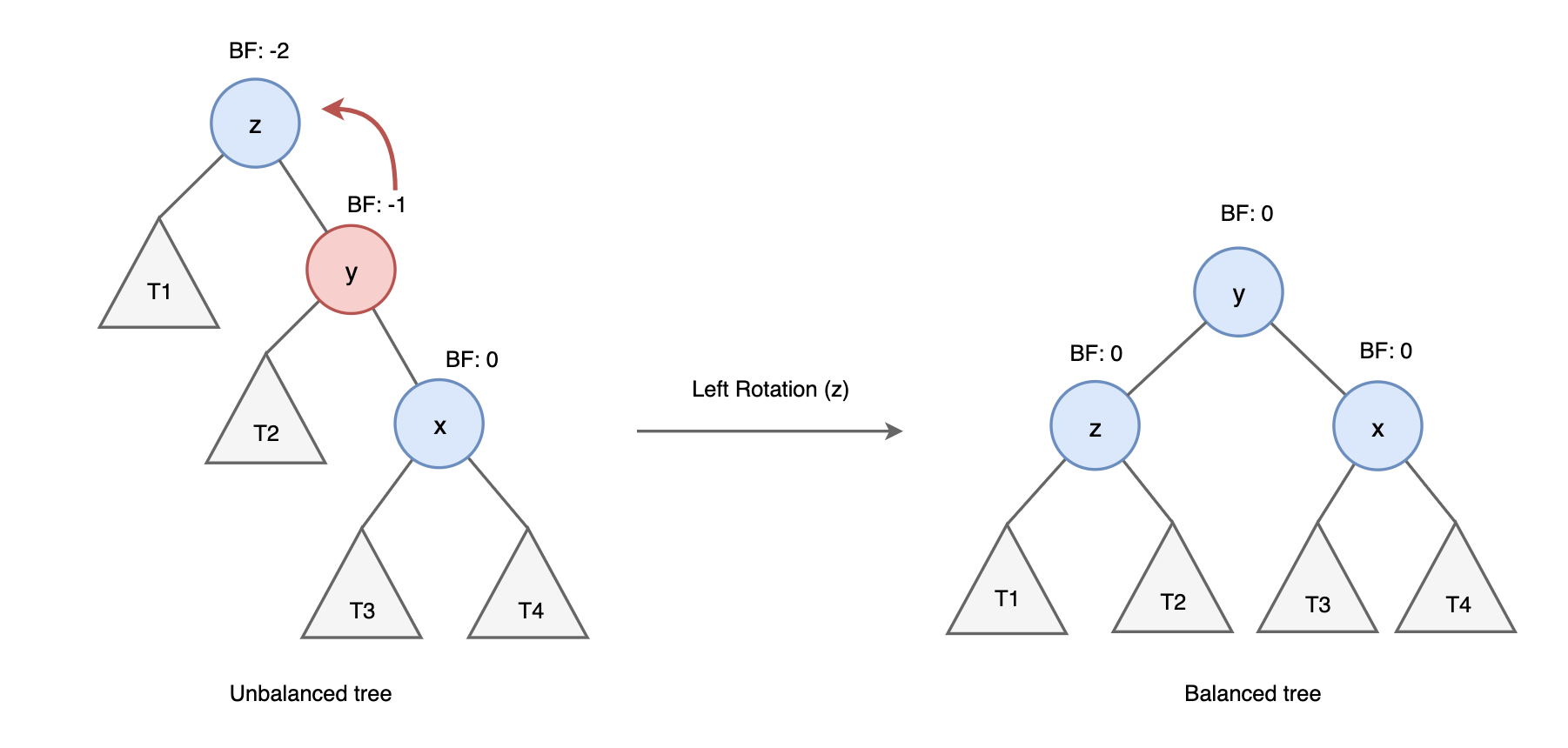
- 각 노드의 BF를 [-1,0,1] 만 가지게 하여 균형을 유지
- BF(Balance Factor) : 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
AVL 트리 - 리밸런싱
- 균형이 깨진 경우
- BF가 ‘+’ 이면 왼쪽 서브트리에 이상 있음
- BF가 ‘-‘ 이면 오른쪽 서브트리에 이상 있음
- 회전 연산
- 단순 회전 : LL, RR
- 이중 회전 : LR, RL
AVL 트리 - LL(Left-Left)
- 오른쪽 방향으로 1회 회전

AVL 트리 - RR(Right-Right)
- 왼쪽 방향으로 1회 회전
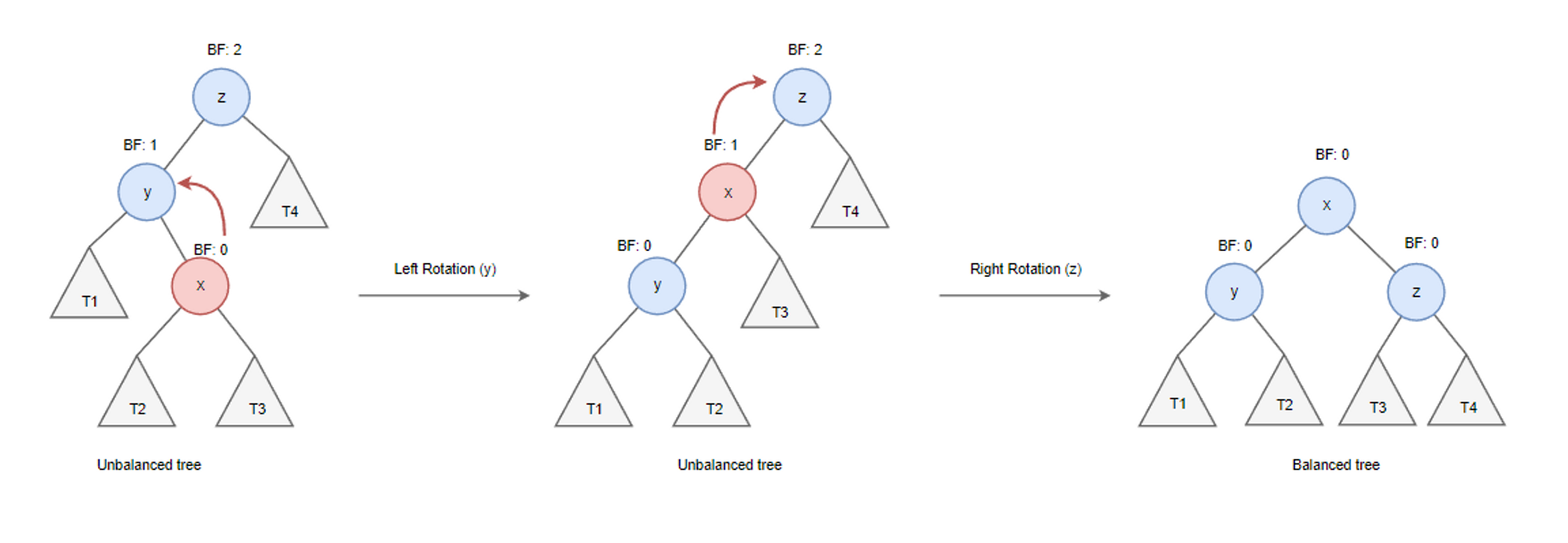
AVL 트리 LR(Left-Right)
- RR 회전 후 LL 회전
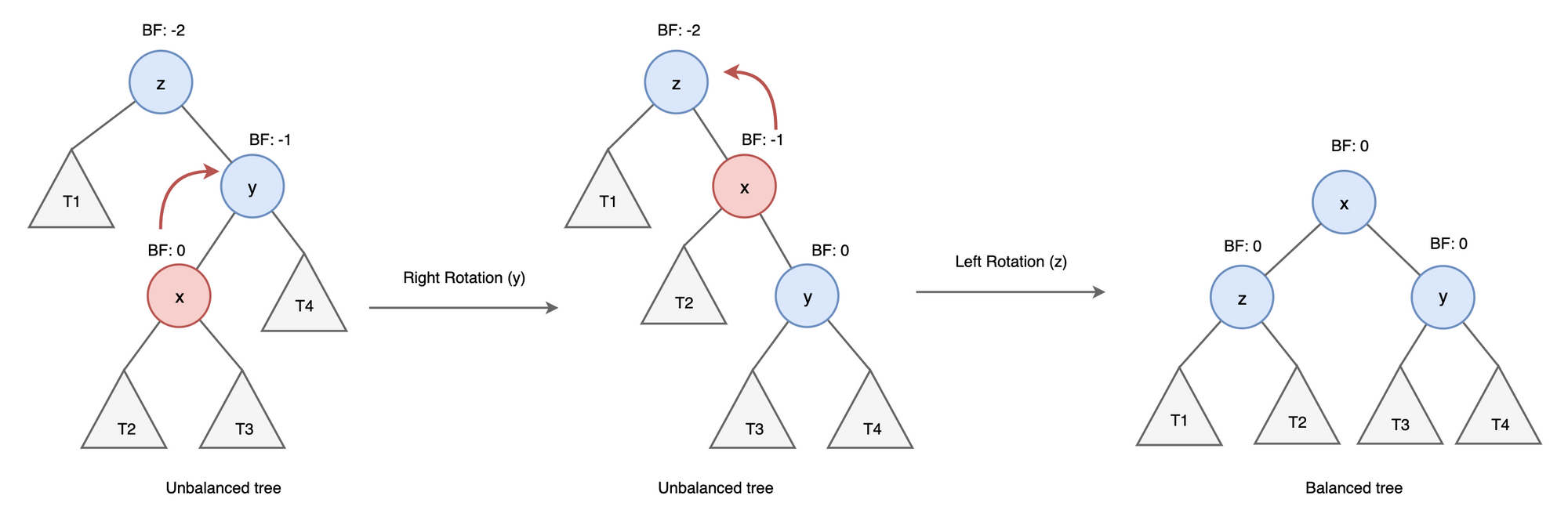
AVL 트리 RL(Right-Left)
- LL회전 후 RR 회전
AVL 트리 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
class Node {
int key;
int height;
Node left;
Node right;
public Node(int key, Node left, Node right) {
this.key = key;
this.height = 0;
this.left = left;
this.right = right;
}
}
class AVLTree {
Node head;
//높이 정보
public int height(Node node) {
if (node == null) {
return -1;
}
return node.height;
}
// LL case
public Node rightRotate(Node node) {
Node lNode = node.left;
node.left = lNode.right;
lNode.right = node;
node.height = Math.max(height(node.left), height(node.right)) + 1;
lNode.height = Math.max(height(lNode.left), height(lNode.right)) + 1;
return lNode;
}
// RR case
public Node leftRotate(Node node) {
Node rNode = node.right;
node.right = rNode.left;
rNode.left = node;
node.height = Math.max(height(node.left), height(node.right)) + 1;
rNode.height = Math.max(height(rNode.left), height(rNode.right)) + 1;
return rNode;
}
// LR case
public Node lrRotate(Node node) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// RL case
public Node rlRotate(Node node) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
//BF 계산
public int getBalance(Node node) {
if (node == null) {
return 0;
}
return height(node.left) - height(node.right);
}
//데이터 추가(BF정보까지 체크)
public void insert(int key) {
this.head = insert(this.head, key);
}
public Node insert(Node node, int key) {
if (node == null) {
return new Node(key, null, null);
}
if (key < node.key) {
node.left = insert(node.left, key);
} else {
node.right = insert(node.right, key);
}
node.height = Math.max(height(node.left), height(node.right)) + 1;
int balance = getBalance(node);
if (balance > 1 && key < node.left.key) { //LL
return rightRotate(node);
}
if (balance < -1 && key > node.right.key) { //RR
return leftRotate(node);
}
if (balance > 1 && key > node.left.key) { //LR
return lrRotate(node);
}
if (balance < -1 && key < node.right.key) { //RL
return rlRotate(node);
}
return node;
}
//데이터 삭제
public void delete(int key) {
this.head = delete(this.head, key);
}
public Node delete(Node node, int key) {
if (node == null) {
return null;
}
if (key < node.key) {
node.left = delete(node.left, key);
} else if (key > node.key) {
node.right = delete(node.right, key);
} else {
if (node.left == null) {
return node.right;
} else if (node.right == null) {
return node.left;
} else {
Node predecessor = node;
Node successor = node.left;
while (successor.right != null) {
predecessor = successor;
successor = successor.right;
}
predecessor.right = successor.left;
node.key = successor.key;
}
}
node.height = Math.max(height(node.left), height(node.right)) + 1;
int balance = getBalance(node);
if (balance > 1 && getBalance(node.left) > 0) { //LL
return rightRotate(node);
}
if (balance < -1 && getBalance(node.right) < 0) { //RR
return leftRotate(node);
}
if (balance > 1 && getBalance(node.left) < 0) { //LR
return lrRotate(node);
}
if (balance < -1 && getBalance(node.right) > 0) { //RL
return rlRotate(node);
}
return node;
}
}
Red-Black 트리
- 조건
- root 노드와 leaf 노드의 색은 black (RB Tree 에서는 Null Node가 leaf 노드)
- red색 노드의 자식은 black(double red 불가)
- 모든 leaf 노드에서 root 노드까지 가는 경로 black 수는 같음
- 조건이 깨지는 상황에서 Rebalancing

NIL : RB Tree의 leaf node (규칙을 위한 노드, Null Node라고 이해)
Red-Black 트리 - 삽입
-
case1) 노드 삽입 후 double red발생 : 부모 노드의 형제 노드가 red일 때
-
Recoloring 진행
- 삽입한 노드의 부모와 부모 형제 노드를 black으로 변경
- 부모의 부모 노드를 red로 변경
- 부모의 부모 노드가 root인지 double red인지에 따라 조정 진행
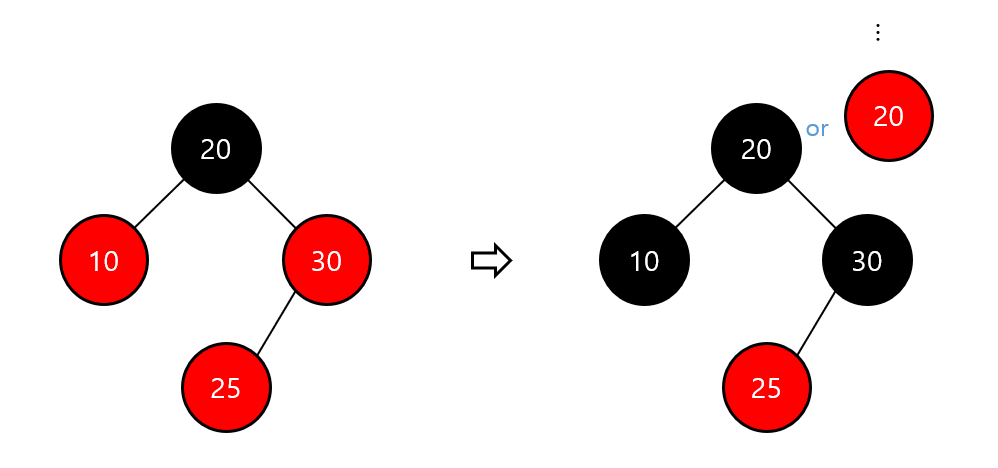
- case2) 노드 삽입 후 double red발생 : 부모 노드의 형제 노드가 black이거나 없을 때
- Restructuring 진행
- 조정 대상 : 삽입한 노드, 부모 노드, 부모의 부모 노드
- 조정 대상 노드들을 오름차순 정렬
- 가운데 노드를 부모 노드로 선정하고 black으로 변경
- 나머지 두 노드를 자식 노드로 두고 red 변경
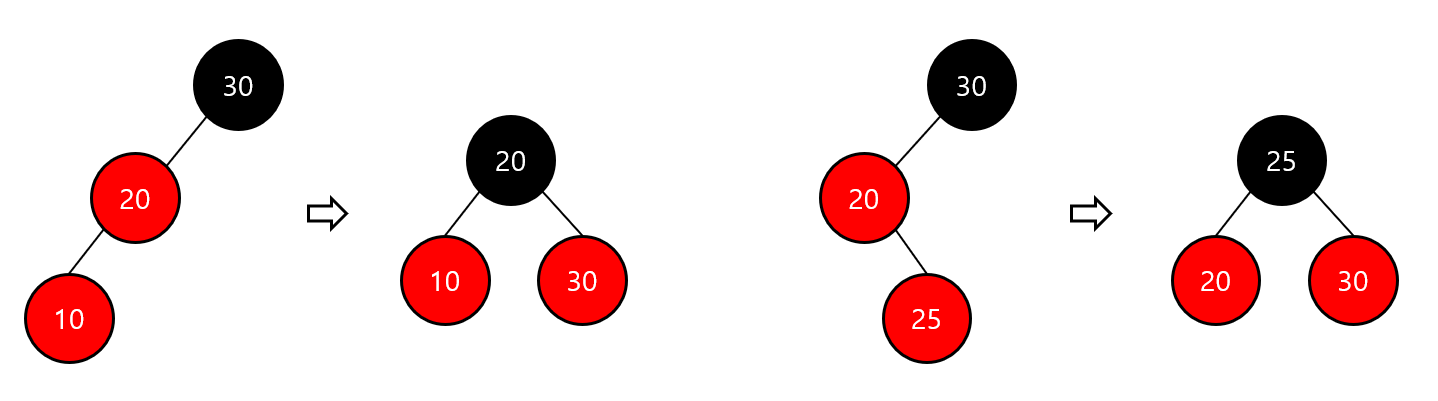
Red-Black 트리 - 삭제
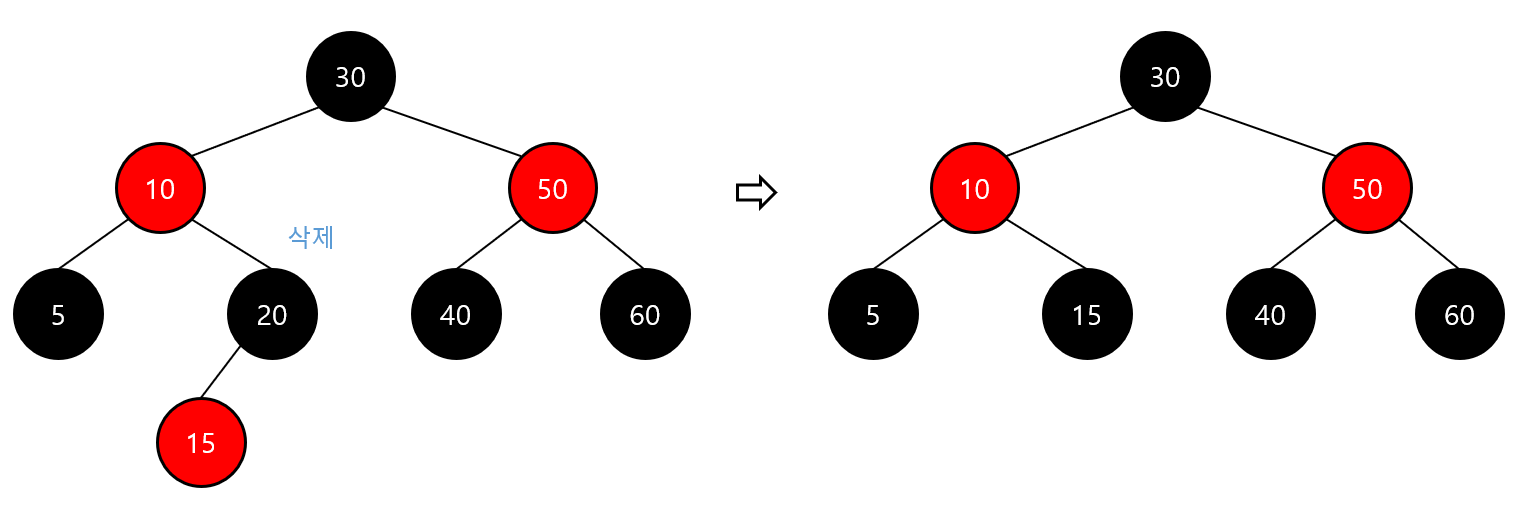
- 삭제 대상 노드가 Black 이고 그 자리에 오는 노드가 red인 경우
- 해당 자리로 오는 red 노드를 black으로 변경
이중 흑색
- 삭제 대상의 노드가 black, 그 자리에 오는 노드가 black인 경우(Double black case)
- case1) 이중 흑색 노드의 형제 노드가 black이고 형제의 양쪽 자식이 모두 black인 경우
- 형제 노드를 red 변경
- 이중 흑색 노드의 검은색 1개를 부모 노드로 전달
- 부모가 root가 아닌 이중 흑색 노드가 되면 해당 반복 진행
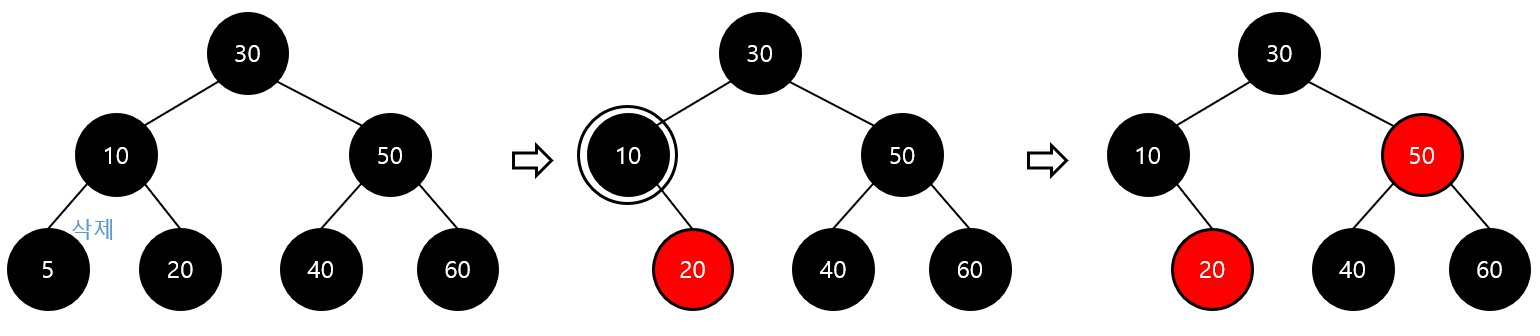
- case2) 이중 흑색 노드의 형제 노드가 red인 경우
- 형제 노드를 black 변경
- 부모 노드를 red변경
- 부모 노드를 기준으로 왼쪽으로 회전
- 그 다음 이중 흑색 case에 따라 반복 진행
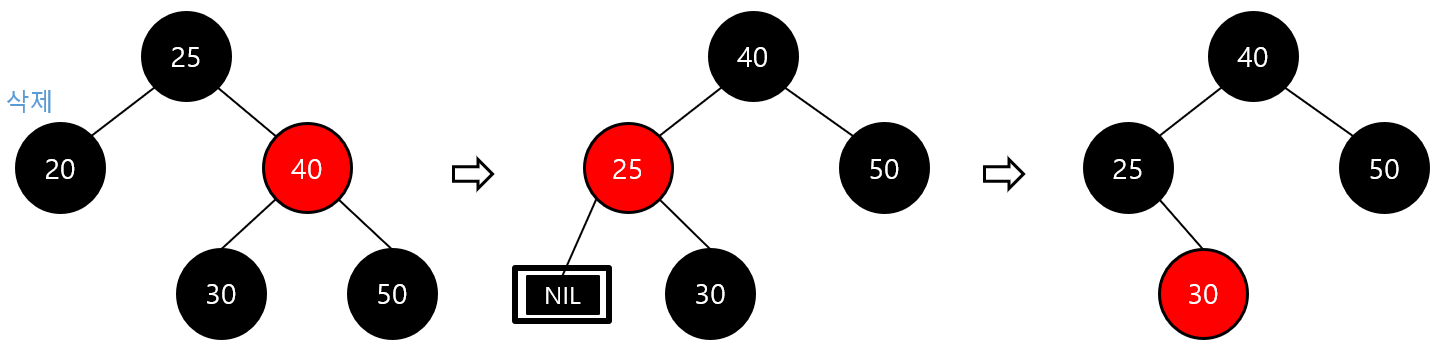
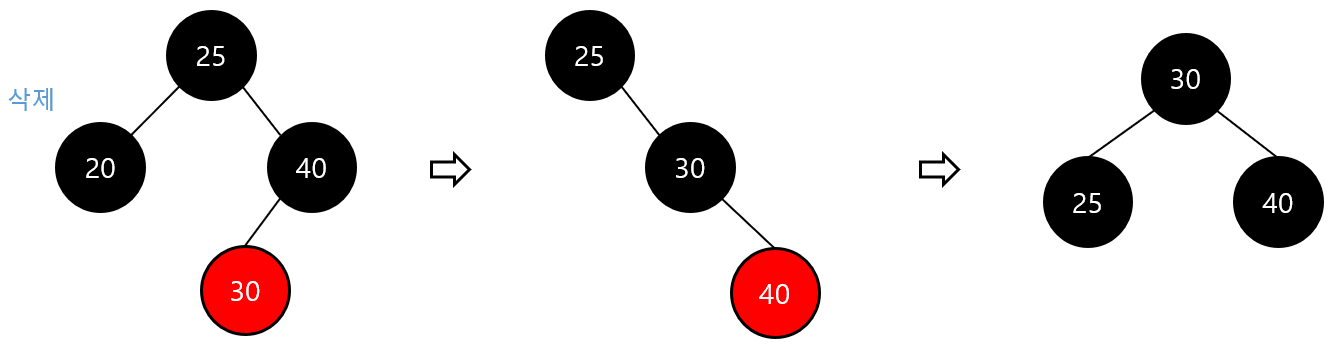
- case3-1) 이중 흑색 노드 형제 노드가 black 이고 오른쪽 자식이 red인 경우
- 부모 노드와 형제 노드의 오른쪽 자식 노드를 검은색으로 변경
- 부모 노드를 기준으로 왼쪽으로 회전
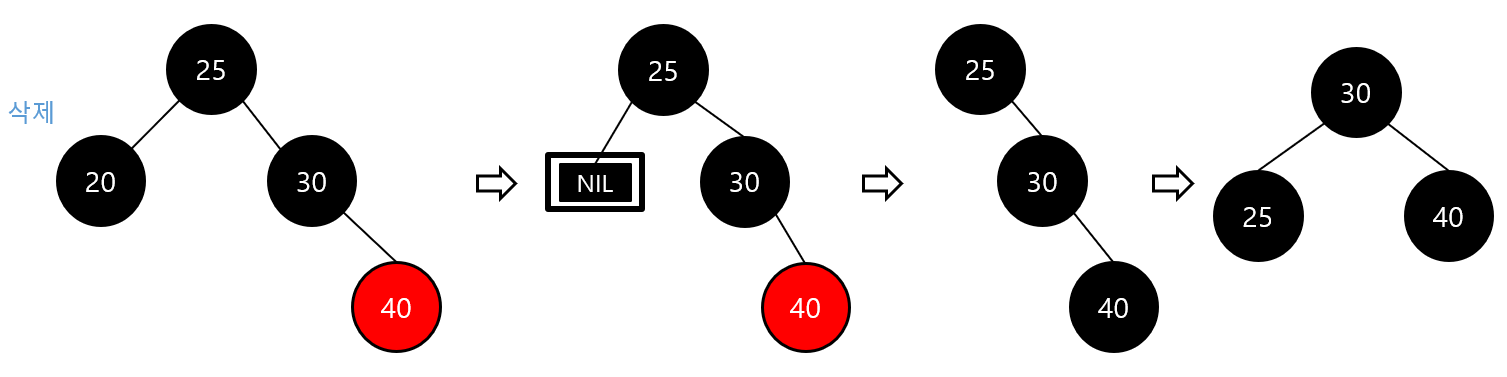
- case3-2) 이중 흑색 노드의 형제 노드가 black 이고 왼쪽 자식이 red인 경우
- 형제 노드를 red로 변경
- 형제 노드의 왼쪽 자식 노드를 black으로 변경
- 형제 노드를 기준으로 오른쪽으로 회전 후 3-1 case 진행
Red-Black 트리 구현
- 삽입 과정만 진행
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
class Node {
int key;
int color;
Node left;
Node right;
Node parent;
public Node(int key, int color, Node left, Node right, Node parent) {
this.key = key;
this.color = color;
this.left = left;
this.right = right;
this.parent = parent;
}
}
class RedBlackTree {
final int BLACK = 0;
final int RED = 1;
Node head;
public void insert(int key) {
Node checkNode = null;
if (this.head == null) {
this.head = new Node(key, BLACK, null, null, null);
} else {
Node cur = this.head;
while (true) {
Node pre = cur;
if (key < cur.key) {
cur = cur.left;
if (cur == null) {
pre.left = new Node(key, RED, null, null, pre);
checkNode = pre.left;
break;
}
} else {
cur = cur.right;
if (cur == null) {
pre.right = new Node(key, RED, null, null, pre);
checkNode = pre.right;
break;
}
}
}
reBalance(checkNode);
}
}
public void reBalance(Node node) {
while (node.parent != null && node.parent.color == RED) {
Node sibling = null;
if (node.parent == node.parent.parent.left) {
sibling = node.parent.parent.right;
} else {
sibling = node.parent.parent.left;
}
//부모의 형제노드가 RED 일 경우 Recoloring
if (sibling != null && sibling.color == RED) {
node.parent.color = BLACK;
sibling.color = BLACK;
node.parent.parent.color = RED;
if (node.parent.parent == this.head) {
node.parent.parent.color = BLACK;
break;
} else {
node = node.parent.parent;
continue;
}
} else { //Restructuring
if (node.parent == node.parent.parent.left) {
if (node == node.parent.right) {
node = node.parent;
leftRotate(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
rightRotate(node.parent.parent);
} else if (node.parent == node.parent.parent.right) {
if (node == node.parent.left) {
node = node.parent;
rightRotate(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
leftRotate(node.parent);
}
}
}
}
public void leftRotate(Node node) {
if (node.parent == null) {
Node rNode = this.head.right;
this.head.right = rNode.left;
rNode.left.parent = this.head;
this.head.parent = rNode;
rNode.left = this.head;
rNode.parent = null;
this.head = rNode;
} else {
if (node == node.parent.left) {
node.parent.left = node.right;
} else {
node.parent.right = node.right;
}
node.right.parent = node.parent;
node.parent = node.right;
if (node.right.left != null) {
node.right.left.parent = node;
}
node.right = node.right.left;
node.parent.left = node;
}
}
public void rightRotate(Node node) {
if (node.parent == null) {
Node lNode = this.head.left;
this.head.left = lNode.right;
lNode.right.parent = this.head;
this.head.parent = lNode;
lNode.right = this.head;
lNode.parent = null;
this.head = lNode;
} else {
if (node == node.parent.left) {
node.parent.left = node.left;
} else {
node.parent.right = node.left;
}
node.left.parent = node.parent;
node.parent = node.left;
if (node.left.right != null) {
node.left.right.parent = node;
}
node.left = node.left.right;
node.parent.right = node;
}
}
}
AVL트리 vs Red-Black 트리
- 시간복잡도 : 둘다 O(logN)
- 균형 수준
- AVL 트리가 Red-Black 트리 보다 좀 더 엄격하게 균형 잡음
- Red-Black 트리는 색으로 구분하는 경우로 인해 회전 수 감소
- 실 사용시
- Tree 체계가 잡힌 후 탐색이 많은 경우에는 AVL 트리가 유리
- 삽입 삭제가 빈번한 경우에는 Red-Black 트리가 유리

댓글남기기