[알고리즘] 정렬
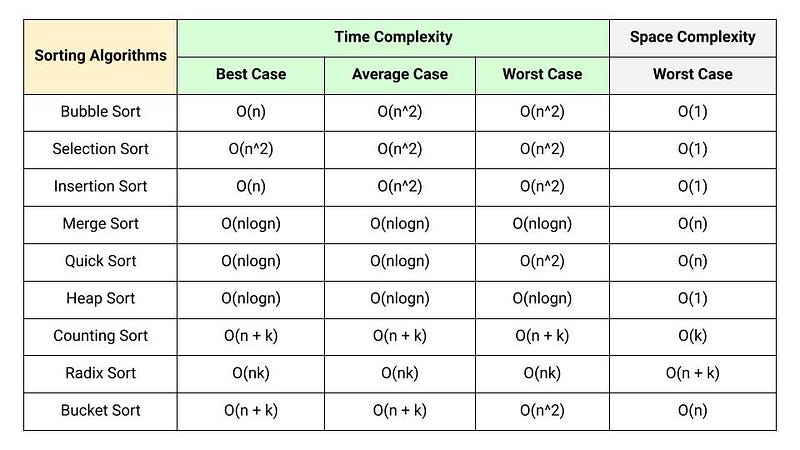
정렬(Sorting)
-
특정 값을 기준으로 데이터를 순서대로 배치하는 방법
- 구현 난이도는 쉽지만 속도는 느린 알고리즘
- 버블 정렬, 삽입 정렬, 선택 정렬
- 구현 난이도는 조금 어렵지만 속도는 빠른 알고리즘
- 합병 정렬, 힙 정렬, 퀵 정렬, 트리 정렬
- 하이브리드 정렬
- 팀 정렬, 블록 병합 정렬, 인트로 정렬
- 기타 정렬 알고리즘
- 기수 정렬, 카운팅 정렬,셸 정렬,보고 정렬
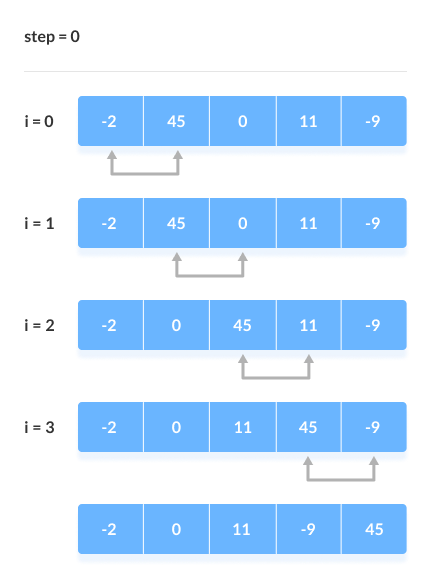
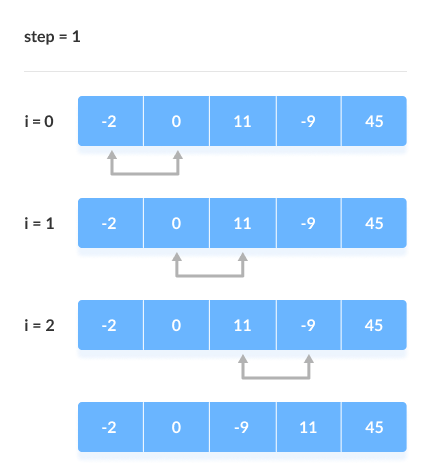
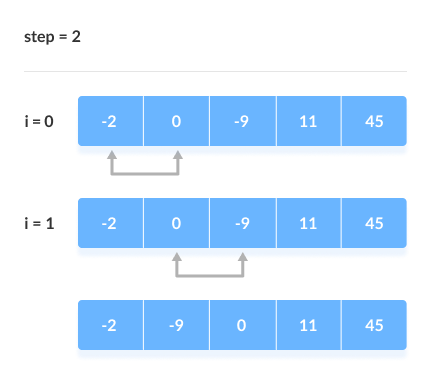
버블 정렬(Bubble sort)
- 인접한 데이터를 비교하며 자리 바꾸는 방식
- 알고리즘 복잡도: O(n2)
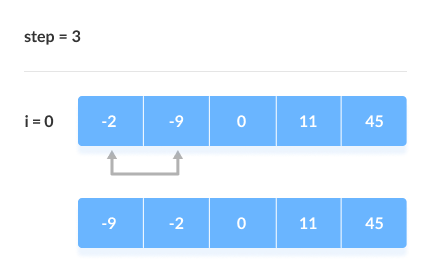
- 버블 정렬 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class BubbleSort {
public static void bubbleSort(int[] arr) {
// case 1
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
// case 2
for (int i = 1; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
}
삽입 정렬(Insertion Sort)
- 앞의 데이터를 정렬 해가면서 삽입 위치를 찾아 정렬하는 방식
- 알고리즘 복잡도: O(n2)
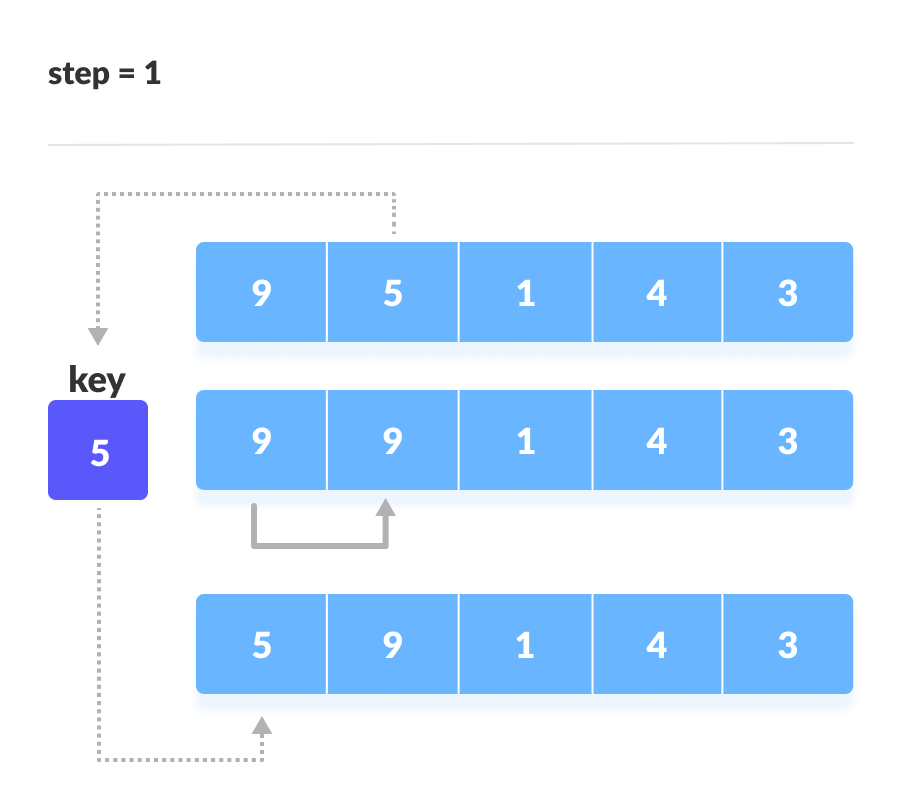
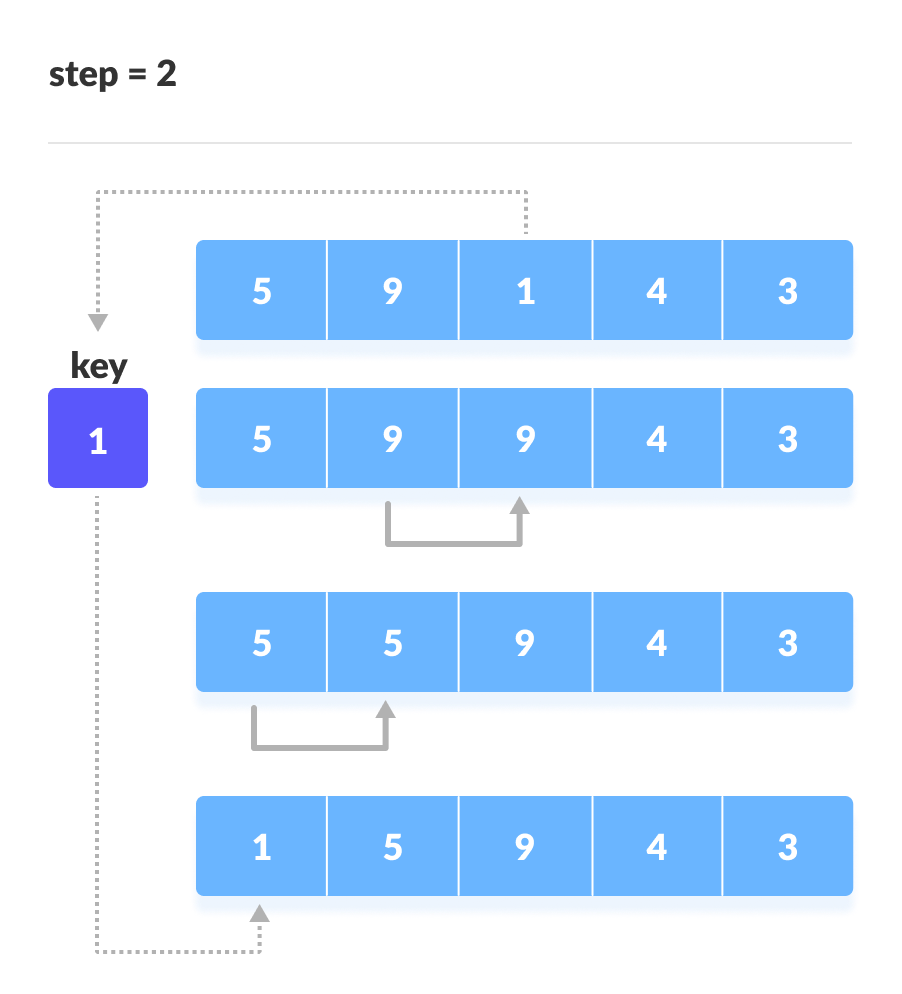
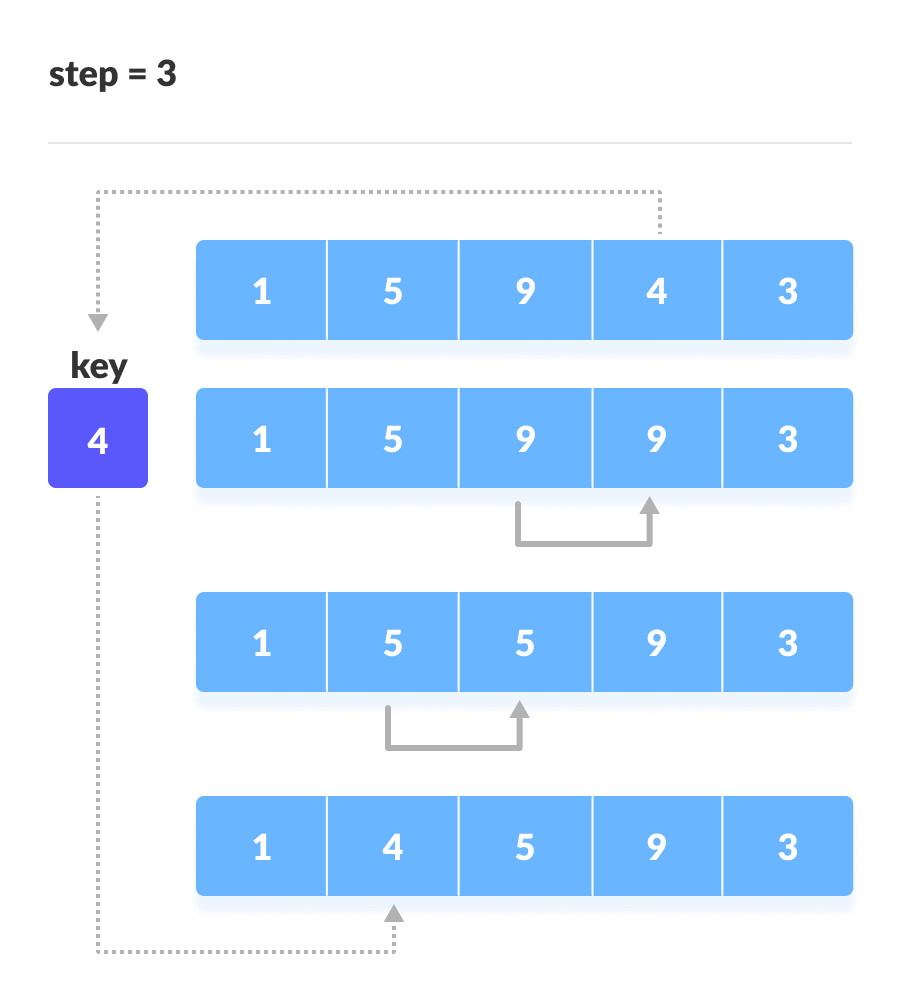
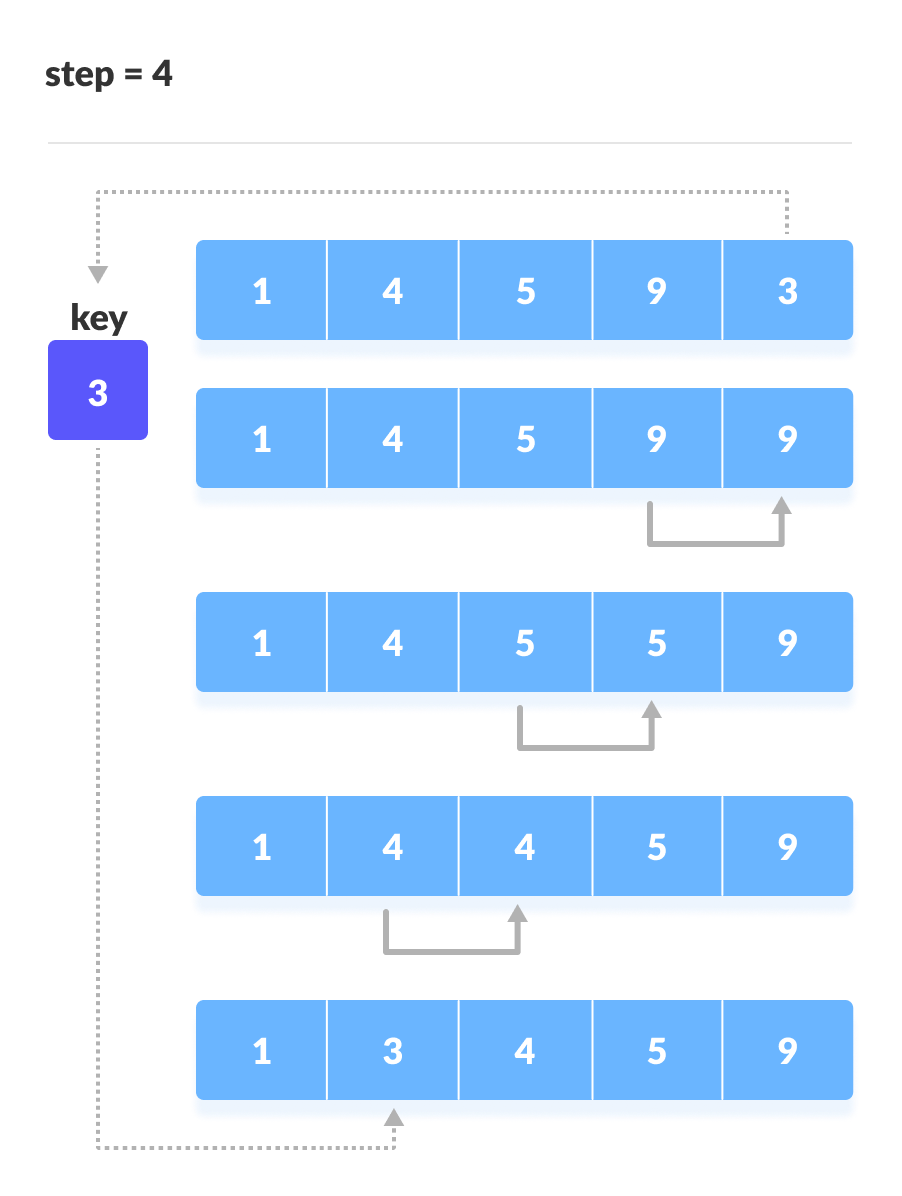
- 삽입 정렬 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class InsertionSort {
public static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
int tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
} else{
break;
}
}
}
}
}
선택 정렬(Selection Sort)
- 최소 또는 최대 값을 찾아서 가장 앞 또는 뒤부터 정렬하는 방식
- 알고리즘 복잡도: O(n2)
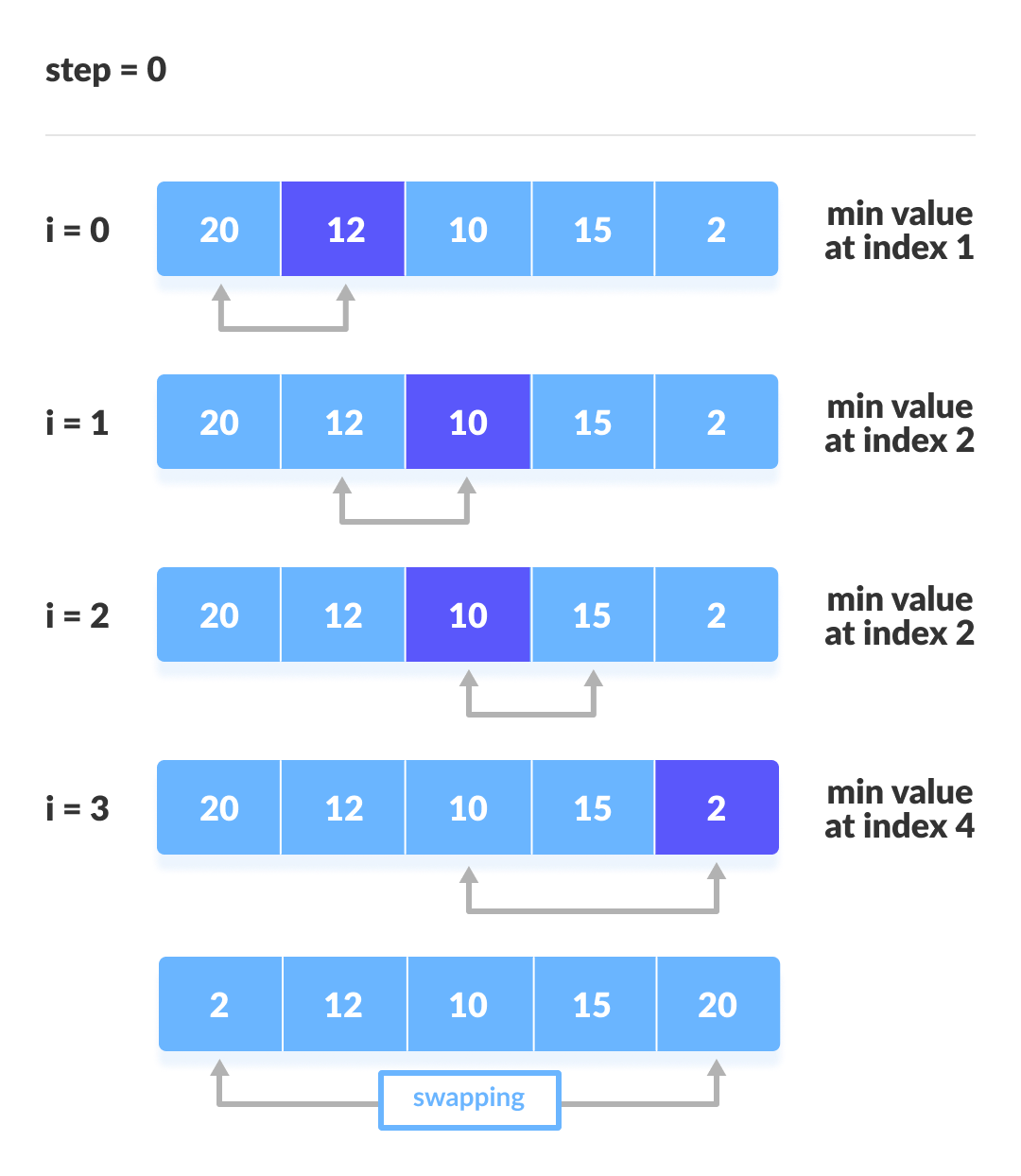
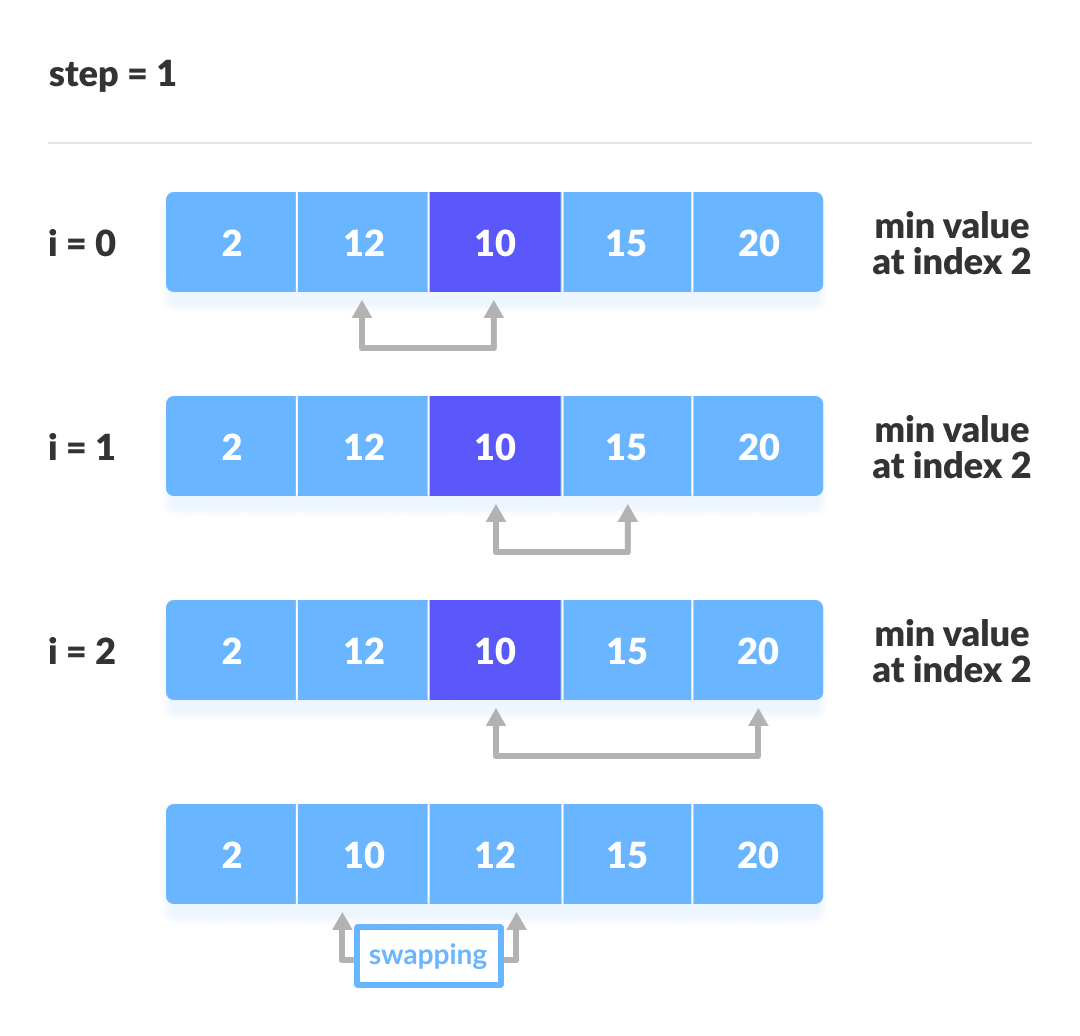
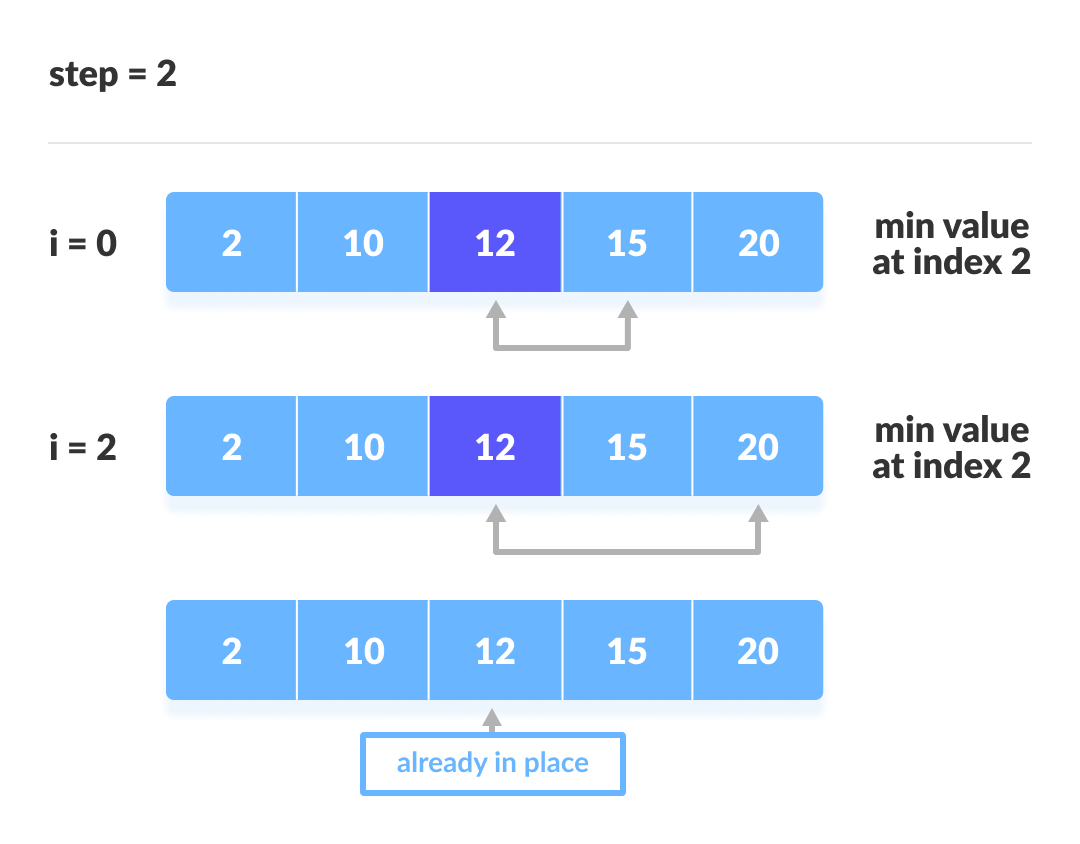
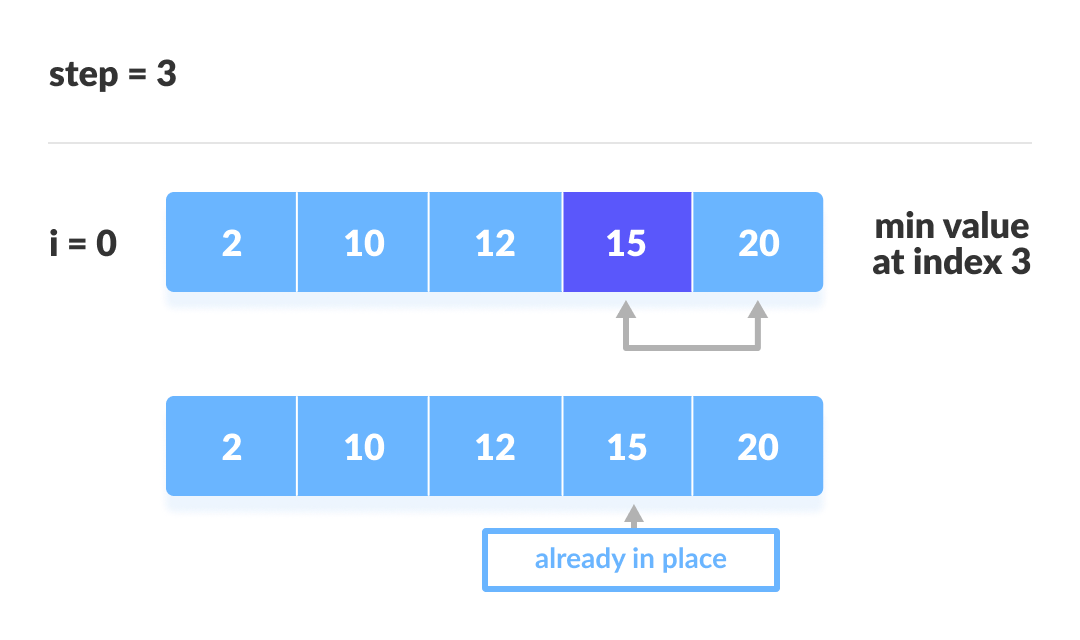
- 선택 정렬 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class SelectionSort {
public static void selectionSort(int[] arr) {
// case 1: 최소값을 찾아서 앞쪽의 데이터와 교환
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
// case 2: 최대값을 찾아서 뒤쪽의 데이터와 교환
for (int i = arr.length - 1; i > 0; i--) {
int max = i;
for (int j = i - 1; j >= 0; j--) {
if (arr[j] > arr[max]) {
max = j;
}
}
int tmp = arr[i];
arr[i] = arr[max];
arr[max] = tmp;
}
}
}
합병 정렬(Merge Sort)
- 배열을 계속 분할하여 길이가 1이 되도록 만들고 인접한 부분끼리 정렬하면서 합병하는 방식
- 알고리즘 복잡도: O(nlogN)
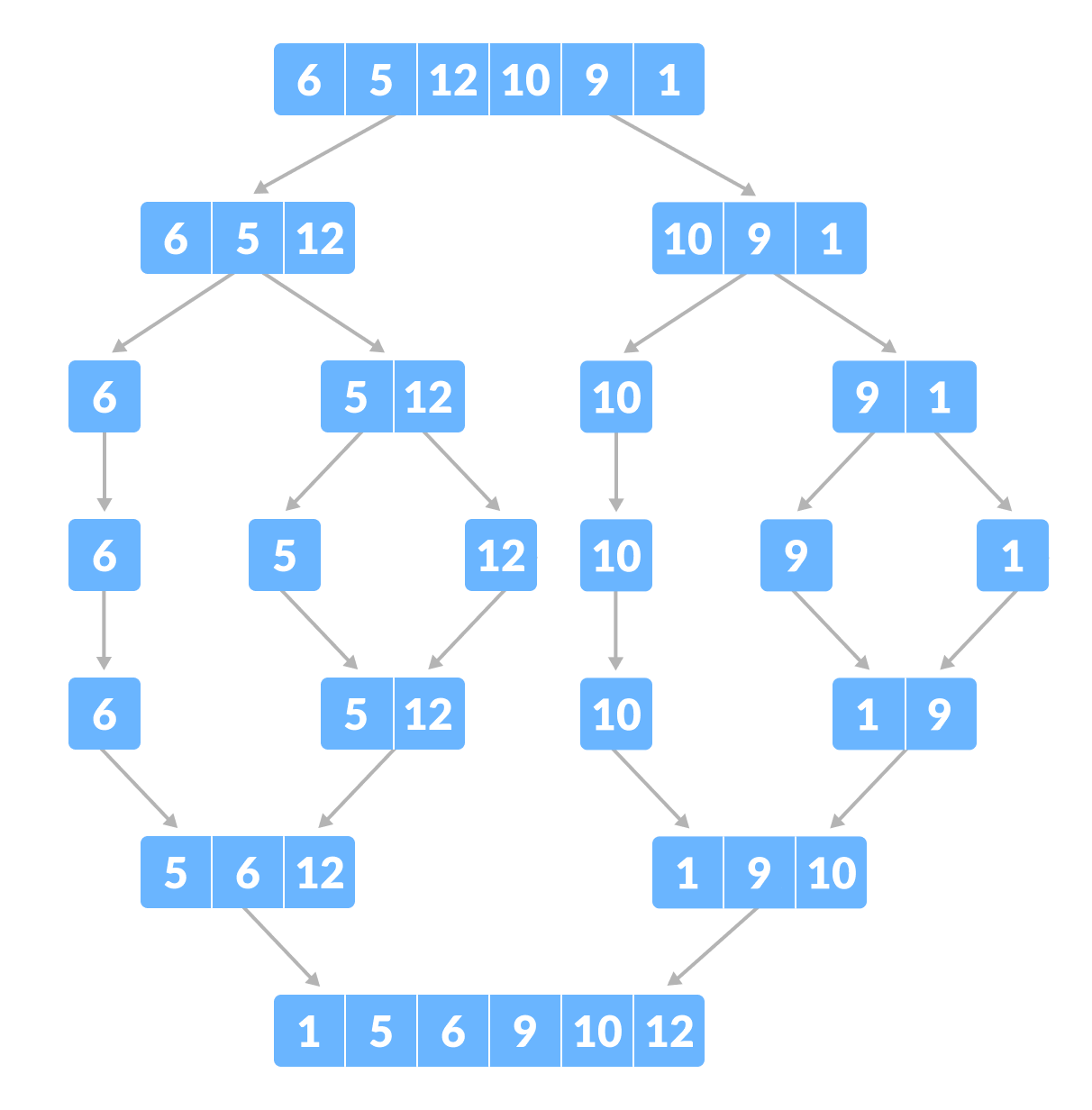
- 합병 정렬 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class MergeSort {
public static void mergeSort(int[] arr, int[] tmp, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, tmp, left, mid);
mergeSort(arr, tmp, mid + 1, right);
merge(arr, tmp, left, right, mid);
}
}
public static void merge(int[] arr, int[] tmp, int left, int right, int mid) {
int p = left;
int q = mid + 1;
int idx = p;
while (p <= mid || q <= right) {
if (p <= mid && q <= right) {
if (arr[p] <= arr[q]) {
tmp[idx++] = arr[p++];
} else {
tmp[idx++] = arr[q++];
}
} else if (p <= mid && q > right) {
tmp[idx++] = arr[p++];
} else {
tmp[idx++] = arr[q++];
}
}
for (int i = left; i <= right; i++) {
arr[i] = tmp[i];
}
}
}
힙 정렬(Heap Sort)
- 힙 자료구조 형태의 정렬 방식
- 기존 배열을 최대 힙으로 구조 변경 후 정렬 진행
-
알고리즘 복잡도:O(nlogN)
- 힙 정렬 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public class HeapSort {
public static void heapSort(int[] arr) {
for (int i = arr.length / 2 - 1; i >= 0; i--) {
heapify(arr, i, arr.length);
}
for (int i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i);
heapify(arr, 0, i);
}
}
public static void heapify(int[] arr, int parentIdx, int size) {
int leftIdx = 2 * parentIdx + 1;
int rightIdx = 2 * parentIdx + 2;
int maxIdx = parentIdx;
if (leftIdx < size && arr[maxIdx] < arr[leftIdx]) {
maxIdx = leftIdx;
}
if (rightIdx < size && arr[maxIdx] < arr[rightIdx]) {
maxIdx = rightIdx;
}
if (parentIdx != maxIdx) {
swap(arr, maxIdx, parentIdx);
heapify(arr, maxIdx, size);
}
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
퀵 정렬(Quick Sort)
- 임의의 기준 값(Pivot)을 정하고 그 값을 기준으로 좌우로 분할하며 정렬하는 방식
- 알고리즘 복잡도: O(n2)
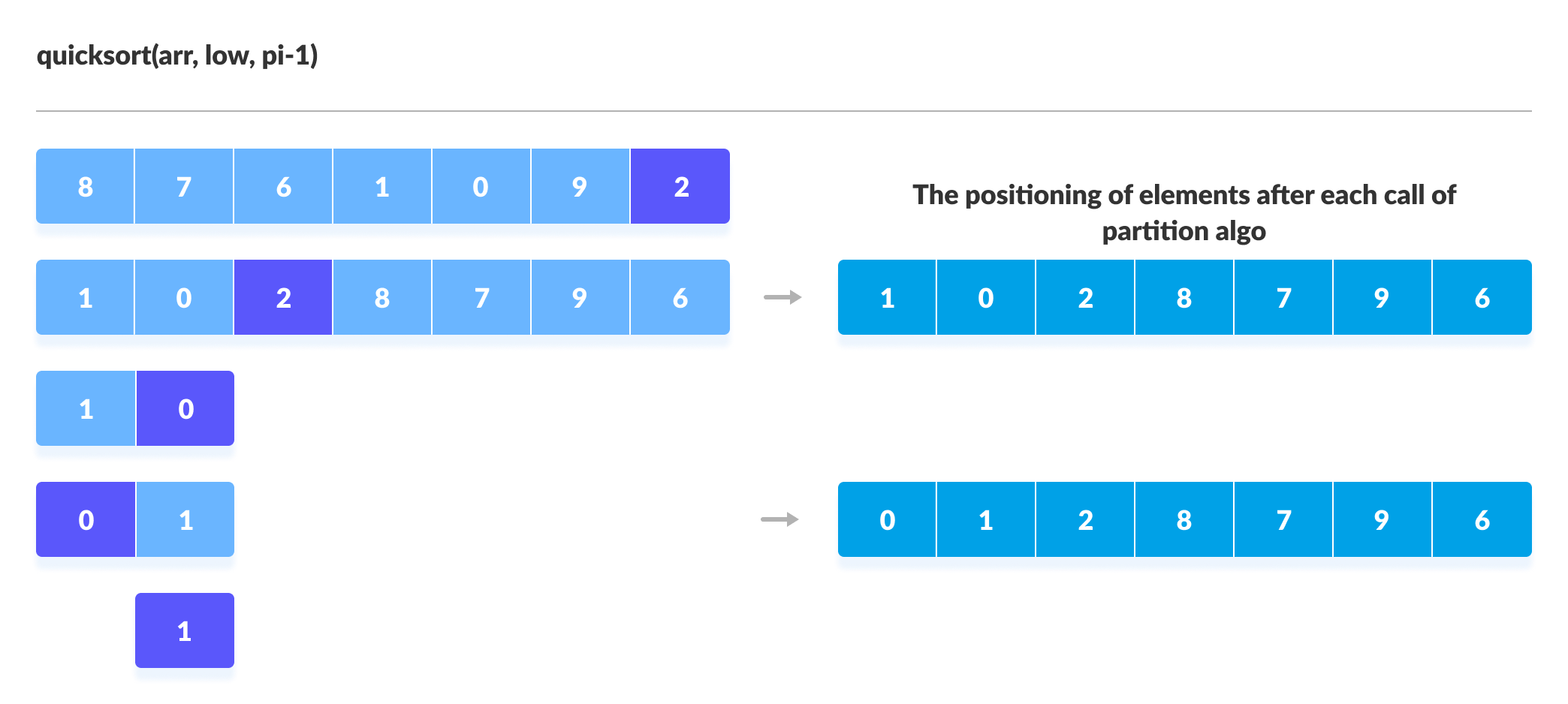
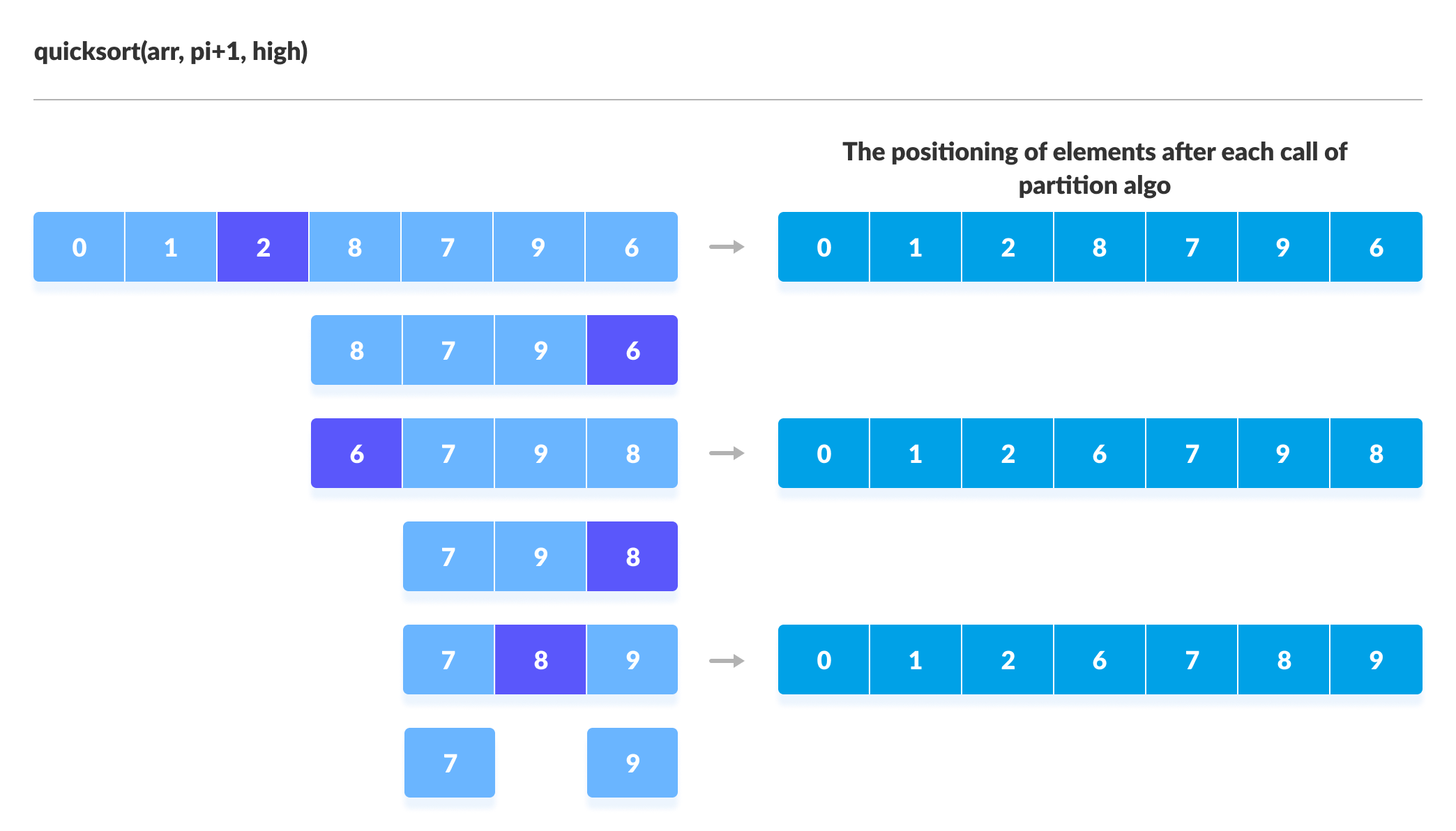
- 퀵 정렬 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public class QuickSort {
public static void quickSort(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int pivot = partition(arr, left, right);
quickSort(arr, left, pivot - 1);
quickSort(arr, pivot + 1, right);
}
public static int partition(int[] arr, int left, int right) {
int pivot = arr[left];
int i = left;
int j = right;
while (i < j) {
while (arr[j] > pivot && i < j) {
j--;
}
while (arr[i] <= pivot && i < j) {
i++;
}
swap(arr, i, j);
}
swap(arr,left,i);
return i;
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
트리 정렬(Tree Sort)
- 이진 탐색 트리(BST)를 만들어서 정렬하는 방식
- 알고리즘 복잡도 O(logN)
기수 정렬(Radix Sort)
- 낮은 자리 수부터 정렬하는 방식
- 각 원소 간의 비교 연산을 하지 않아 빠른 대신 기수 테이블을 위한 메모리 필요
- 알고리즘 복잡도 : O(dn)
- d:최대 자리수
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class RadixSort {
public static void radixSort(int[] arr) {
//기수 테이블 생성
ArrayList<Queue<Integer>> list = new ArrayList<>();
for (int i = 0; i < 10; i++) {
list.add(new LinkedList<>());
}
int idx = 0;
int div = 1;
int maxLen = getMaxLen(arr);
for (int i = 0; i < maxLen; i++) {
for (int j = 0; j < arr.length; j++) {
list.get((arr[j] / div) % 10).offer(arr[j]);
}
for (int j = 0; j < 10; j++) {
Queue<Integer> queue = list.get(j);
while (!queue.isEmpty()) {
arr[idx++] = queue.poll();
}
}
idx = 0;
div *= 10;
}
}
}
계수 정렬(Counting Sort)
- 숫자끼리 비교하지 않고 카운트를 세서 정렬하는 방식
- 카운팅을 위한 메모리 필요
- 알고리즘 복잡도:O(n+k)
- k:정렬 대상 데이터 중 최대 값
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class CountingSort {
public static void countingSort(int[] arr) {
int max = Arrays.stream(arr).max().getAsInt();
int[] cntArr = new int[max + 1];
for (int i = 0; i < arr.length; i++) {
cntArr[arr[i]]++;
}
int idx = 0;
for (int i = 0; i < cntArr.length; i++) {
while (cntArr[i] > 0) {
arr[idx++] = i;
cntArr[i] -= 1;
}
}
//배열 사용시 메모리가 너무 커질 수도있으니 HashMap을 사용시 더 좋을 수 있다.
HashMap<Integer, Integer> map = new HashMap<>();
for (int item : arr) {
map.put(item, map.getOrDefault(item, 0) + 1);
}
int idx2 = 0;
ArrayList<Integer> list = new ArrayList<>(map.keySet());
Collections.sort(list);
for (int i = 0; i < list.size(); i++) {
int cnt = map.get(list.get(i));
while (cnt > 0) {
arr[idx2++] = list.get(i);
cnt--;
}
}
}
}
셸 정렬(Shell Sort)
- 삽입 정렬의 약점 보완한 방식
- 삽입 정렬의 약점
- 오름차순 정렬 기준, 내림 차순으로 구성된 데이터에 대해서는 앞의 데이터와 하나씩 비교하며 모두 교환 필요
- 이전의 모든 데이터와 비교하지 않고 일정 간격을 두어 비교
- 알고리즘 복잡도:O(n2)
- 간격 설정에 따라 Worst case는 삽입 정렬과 동일
- 일반적인 산포 데이터 기준으로는 삽입 정렬에 비해 빠르다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class ShellSort {
public static void shellSort(int[] arr) {
int gap = arr.length / 2;
for (int g = gap; g > 0; g /= 2) {
for (int i = g; i < arr.length; i++) {
int tmp = arr[i];
int j = 0;
for (j = i - g; j >= 0; j -= g) {
if (arr[j] > tmp) {
arr[j + g] = arr[j];
} else {
break;
}
}
arr[j + g] = tmp;
}
}
}
}
연습 문제
-
Q1) nums 배열에 3가지 색으로 구분되는 데이터들이 들어 있다.
0은 흰색, 1은 파랑, 2는 빨강이라고 할때 주어진 nums 배열에서 흰색 부터 빨강 순으로 인접하게 정렬시킨 후 출력하는 프로그램을 작성하세요[입출력 예시]
입력: [2, 0, 2, 1, 1, 0]
출력: [0, 0, 1, 1, 2, 2]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Practice1 {
// 계수 정렬( Counting Sort )
public static void solution(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
int[] cntArr = new int[3];
for (int i = 0; i < arr.length; i++) {
cntArr[arr[i]]++;
}
int idx = 0;
for (int i = 0; i < cntArr.length; i++) {
while (cntArr[i] > 0) {
arr[idx++] = i;
cntArr[i] -= 1;
}
}
}
}
-
Q2) 문자열 배열 strs 가 주어졌을 때 anagram 으로 묶어서 출력하는 프로그램을 작성하세요.
anagram 은 철자 순서를 바꾸면 같아지는 문자를 의미한다.
예) elvis <-> lives
nagram 그룹 내에서 출력 순서는 상관 없다.[입출력 예시]
입력: “eat”, “tea”, “tan”, “ate”, “nat”, “bat”
출력: [[eat, tea, ate], [bat], [tan, nat]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Practice2 {
// 문자열을 정렬하여 anagram 인지 확인 ( eat-> ate / tea -> ate )
public static ArrayList<ArrayList<String>> solution(String[] strs) {
if (strs == null || strs.length == 0) {
return new ArrayList<>();
}
HashMap<String, ArrayList<String>> map = new HashMap<>();
for (String s : strs) {
char[] cArr = s.toCharArray();
sort(cArr);
String key = String.valueOf(cArr);
if (!map.containsKey(key)) {
map.put(key, new ArrayList<>());
}
map.get(key).add(s);
}
return new ArrayList<>(map.values());
}
public static void sort(char[] arr) {
// 삽입 정렬 이용
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
char tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
}
}
}
}
}
-
Q3) intervals 라는 구간으로 이루어진 배열이 주어졌을 때 오버랩 되는 구간을 합치는 프로그램을 작성하세요.
[입출력 예시]
입력: [2, 6], [1, 3], [15, 18], [8, 10]
출력: [1, 6] [8, 10] [15, 18]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import java.util.*;
public class Practice3 {
public static ArrayList<int[]> solution(int[][] intervals) {
if (intervals == null || intervals.length < 2) {
return new ArrayList<>();
}
sort(intervals);
ArrayList<int[]> result = new ArrayList<>();
int[] curInterval = intervals[0];
result.add(curInterval);
for (int i = 1; i < intervals.length; i++) {
if (curInterval[1] >= intervals[i][0]) {
curInterval[1] = intervals[i][1];
} else {
curInterval = intervals[i];
result.add(curInterval);
}
}
return result;
}
public static void sort(int[][] intervals) {
quickSort(intervals, 0, intervals.length - 1);
}
public static void quickSort(int[][] arr, int left, int right) {
if (left >= right) {
return;
}
int pivot = partition(arr, left, right);
quickSort(arr, left, pivot - 1);
quickSort(arr, pivot + 1, right);
}
public static int partition(int[][] arr, int left, int right) {
int pivot = arr[left][0];
int i = left;
int j = right;
while (i < j) {
while (arr[j][0] > pivot && i < j) {
j--;
}
while (arr[i][0] <= pivot && i < j) {
i++;
}
swap(arr, i, j);
}
swap(arr, left, i);
return i;
}
public static void swap(int[][] arr, int i, int j) {
int[] tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
-
Q4) 정수 배열 nums 가 주어졌을 때 오름차순으로 정렬하기 위해 배열 내에서 정렬이 필요한 구간의 길이를 출력하는 프로그램을 작성하세요.
[입출력 예시]
입력: 2, 6, 4, 8, 5, 3, 9, 10 / 출력: 5
입력: 1, 3, 1 / 출력: 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class Practice4 {
public static int solution(int[] nums) {
if (nums == null || nums.length < 2) {
return 0;
}
// 좌측에 변경해야 할 값 찾기
int min = Integer.MAX_VALUE;
int firstIdx = 0;
for (int i = nums.length - 1; i >= 0; i--) {
min = Math.min(min, nums[i]);
if (nums[i] > min) {
firstIdx = i;
}
}
// 우측부터 변경해야 할 값 찾기
int max = Integer.MIN_VALUE;
int lastIdx = -1;
for (int i = 0; i < nums.length; i++) {
max = Math.max(max, nums[i]);
if (nums[i] < max) {
lastIdx = i;
}
}
return lastIdx - firstIdx + 1;
}
}

댓글남기기