[알고리즘] 최단 경로

최단 경로(Shortest Path)

• 가중 그래프 상의 두 노드를 연결하는 가장 짧은 경로를 찾는 방법
• 지도 경로 탐색, 네트워크 구축에 드는 비용을 최소화 하는데 사용
• 최단경로 알고리즘
  • 다익스트라
  • 벨만-포드
  • 플로이드-워셜

다익스트라(Dijkstra)

• 출발점에서 목표점까지의 최단 경로를 구하는 알고리즘
• 한 노드에서 다른 모든 노드로의 최단 경로를 구할 수 있음
• 간선에 음의 가중치가 없어야 함
• 그리디 + DP형태
• 알고리즘 복잡도: O(ElogV) / E :간선수 , V: 노드 수

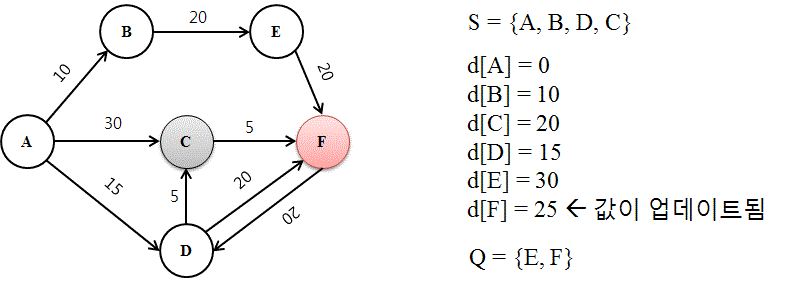
다익스트라 알고리즘 Flow

• 아직 확인하지 않은 거리는 초기값을 Infinity로 설정

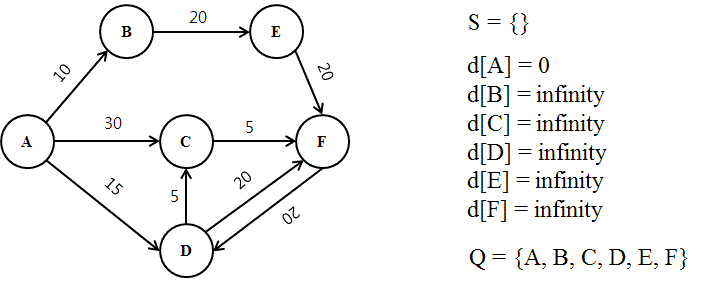
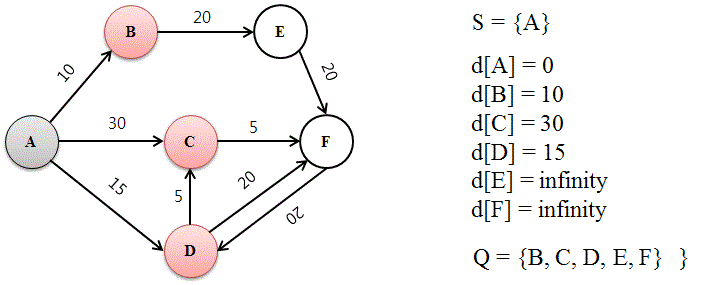
• 루프를 돌려 이웃 노드를 방문 후 거리를 계산

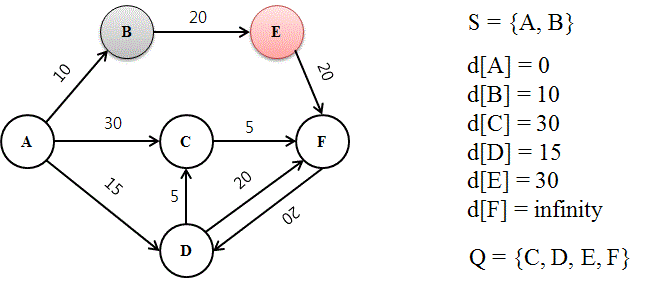
• 최소 경로를 기준으로 다음 목적지 갱신

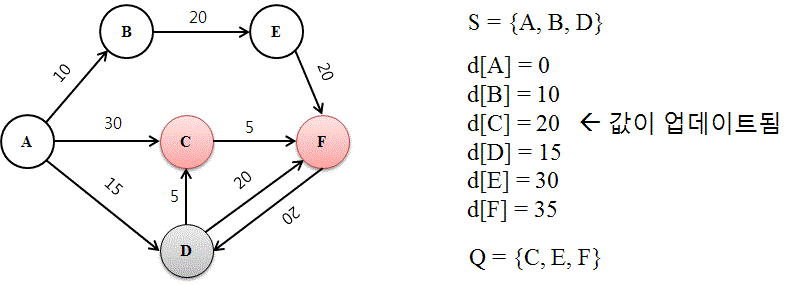
• 새로운 경로가 기존 경로보다 최단 경로 인 경우 값을 업데이트

• 또 다른 루프상황

다익스트라 구현

public class Dijkstra {
    static class Node {
        int to;
        int weight;

        public Node(int to, int weight) {
            this.to = to;
            this.weight = weight;
        }
    }

    public static void dijkstra(int v, int[][] data, int start) {
        // 그래프 생성
        ArrayList<ArrayList<Node>> graph = new ArrayList<>();
        for (int i = 0; i < v + 1; i++) {
            graph.add(new ArrayList<>());
        }

        for (int i = 0; i < data.length; i++) {
            graph.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
        }

        // DP배열 생성 및 다익스트라 구현
        int[] dist = new int[v + 1];
        for (int i = 1; i < v + 1; i++) {
            dist[i] = Integer.MAX_VALUE;
        }
        dist[start] = 0;

        //우선순위 큐 이용
        PriorityQueue<Node> pq = new PriorityQueue<>((x, y) -> x.weight - y.weight);
        pq.offer(new Node(start, 0));

        while (!pq.isEmpty()) {
            Node curNode = pq.poll();

            if (dist[curNode.to] < curNode.weight) {
                continue;
            }

            for (int i = 0; i < graph.get(curNode.to).size(); i++) {
                Node adjNode = graph.get(curNode.to).get(i);

                if (dist[adjNode.to] > curNode.weight + adjNode.weight) {
                    dist[adjNode.to] = curNode.weight + adjNode.weight;
                    pq.offer(new Node(adjNode.to, dist[adjNode.to]));
                }
            }
        }

        // 데이터 출력
        for (int i = 1; i < v + 1; i++) {
            if (dist[i] == Integer.MAX_VALUE) {
                System.out.print("INF ");
            } else {
                System.out.print(dist[i] + " ");
            }
        }
    }
}

벨만-포드(Bellman-Ford)

• 음수 간선이 포함되어 있어도 최단 경로를 구할 수 있음
  • 음수 사이클이 있으면 정상 동작하지 않음
• 매번 모든 간선을 확인하기 때문에 다익스트라에 비해 느림
• 알고리즘 복잡도: O(VE) / E :간선수 , V: 노드 수

벨만-포드 구현

public class BellmanFord {
    static class Edge {
        int from;
        int to;
        int weight;

        public Edge(int from, int to, int weight) {
            this.from = from;
            this.to = to;
            this.weight = weight;
        }
    }

    public static void bellmanFord(int v, int e, int[][] data, int start) {
        Edge[] edge = new Edge[e];
        for (int i = 0; i < e; i++) {
            edge[i] = new Edge(data[i][0], data[i][1], data[i][2]);
        }

        int[] dist = new int[v + 1];
        for (int i = 1; i < v + 1; i++) {
            dist[i] = Integer.MAX_VALUE;
        }
        dist[start] = 0;
        boolean isMinusCycle = false;
        for (int i = 0; i < v + 1; i++) {
            for (int j = 0; j < e; j++) {
                Edge cur = edge[j];

                if (dist[cur.from] == Integer.MAX_VALUE) {
                    continue;
                }

                if (dist[cur.to] > dist[cur.from] + cur.weight) {
                    dist[cur.to] = dist[cur.from] + cur.weight;

                    if (i == v) {
                        isMinusCycle = true;
                    }
                }
            }
        }
        System.out.println("음수 사이클 발생 : " + isMinusCycle);
        for (int i = 1; i < v + 1; i++) {
            if (dist[i] == Integer.MAX_VALUE) {
                System.out.print("INF ");
            } else {
                System.out.print(dist[i] + " ");
            }
        }
        System.out.println();
    }
}

플로이드-워셜(Floyd-Warshall)

• 모든 노드 간의 최단 경로를 구하는 알고리즘
• 음의 간선이 포함되어 있어도 사용 가능
  • 음수 사이클이 있으면 정상 동작 하지 않음
• 알고리즘 복잡도: O(V³)